Konstruktivní geometrie 2024/25
Analytická geometrie v $\mathbb{E}_3$
Analytická geometrie
tzv. souřadnicová či kartézská geometrie, která zkoumá geometrické útvary a vztahy mezi nimi metodami algebry a matematické analýzy
Základní pojmy
- pravotočivá kartézská soustava souřadnic
- bod, vektor
- souřadnice vektoru \[\vec{u}=(u_1,u_2,u_3)\]
- velikost vektoru \[\|\vec{u}\|=\sqrt{u_1^2+u_2^2+u_3^2}\]
skalární součin
- skalární součin dvou nenulových vektorů \[\vec{u}\cdot\vec{v}=u_1v_1+u_2v_2+u_3v_3=\|\vec{u}\|\|\vec{v}\|\cos\varphi\]
- odchylka dvou nenulových vektorů \[\cos\varphi=\frac{\vec{u}\cdot\vec{v}}{\|\vec{u}\|\|\vec{v}\|}\]
vektorový součin
- $\vec{u}\times\vec{v}=(u_2v_3-u_3v_2,u_3v_1-u_1v_3,u_1v_2-u_2v_1)$
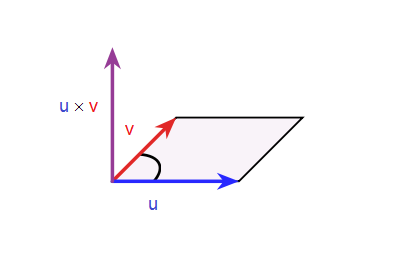
- $\|\vec{u}\times\vec{v}\|=$ obsah rovnoběžníka $\vec{u},\vec{v}$
smíšený součin
- $\vec{u}\cdot(\vec{v}\times\vec{w})=\text{det}(\vec{u},\vec{v},\vec{w})$
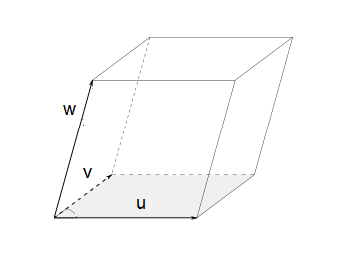
- $\vec{u}\cdot(\vec{v}\times\vec{w})=$ objem rovnoběžnostěnu $\vec{u}, \vec{v}, \vec{w}$
další pojmy
- 2 vektory lineárně závislé $\Leftrightarrow$ určují stejnou přímku $\Leftrightarrow$ kolineární
- 3 vektory lineárně závislé $\Leftrightarrow$ leží v jedné rovině $\Leftrightarrow$ komplanární
Analytický popis základních prvků prostoru
Přímka
jednou rovnicí pouze parametricky!
$X(t)=A+ t\cdot\vec{u}, t\in\mathbb{R}$
jedna přímka má nekonečně mnoho vyjádření v parametrickém tvaru
(zavisí na zvoleném bodu a směrovém vektoru)!
(zavisí na zvoleném bodu a směrovém vektoru)!
Rovina
- obecná rovnice \[ax+by+cz+d=0\]
- úsekový tvar \[\frac{x}{p}+\frac{y}{q}+\frac{z}{r}=1\]
- parametrická rovnice \[X(t,s)=A+t\cdot\vec{u}+s\cdot\vec{v}, s\in\mathbb{R}, t\in\mathbb{R}\]
Rovina - zobrazení
- $\alpha: y = 0$
- $\beta: z = 3$
- $\gamma: 5x + 4y - 20 = 0$
- $\rho: 4x + 3y + 2z - 12 = 0$
- $\sigma: 4x + 3y -2z = 12$
Úmluva: znázorňujeme jen část roviny v prvním oktantu!
Rovina - zobrazení
Určování vzájemné polohy prvků prostoru
Bod $\times$ přímka
Zjistěte, zda bod $M$ leží na přímce $p=(A,\vec{u})$.$M=[2,1,0], A=[1,-1,2], \vec{u}=(1,2,-1)$.
Bod $\times$ přímka
Pomocí rovnice přímky $p$
$p: X(t)=A+t\vec{u}, t\in\mathbb{R}$
rozepsat po souřadnicích $\implies$ soustava rovnic
dosadit bod $M$
vyřešit
dosadit bod $M$
vyřešit
Bod $\times$ přímka
Využitím lineární závislosti vektorů
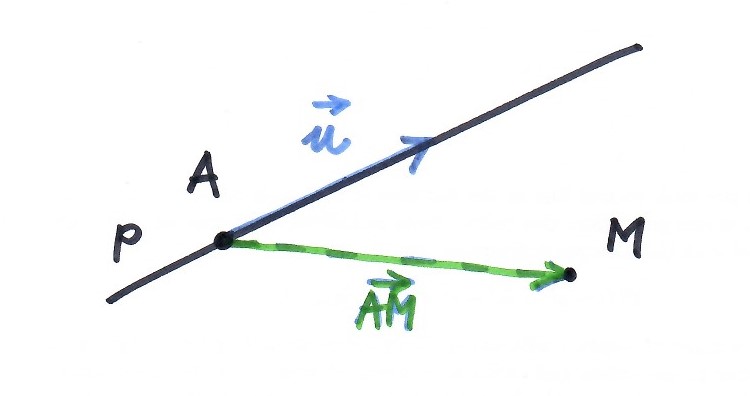
Bod $\times$ přímka
Řešení:
$\vec{AM}=M-A=(1,2,-2) \implies \vec{u}, \vec{AM}\ \text{nekolineární} \implies M\notin p$
přímka $\times$ přímka
Klasicky - podle počtu řešení soustavy 3 rovnic pro 2 neznámé
- nekonečně mnoho řešení (dim 1) $\Leftrightarrow$ přímky totožné
- právě jedno řešení $\Leftrightarrow$ přímky různoběžné
- žádné řešení $\Leftrightarrow$ přímky rovnoběžné nebo mimoběžné
(rozhodnout podle závislosti/nezávislosti směrových vektorů)
přímka $\times$ přímka
Využitím lineární závislosti vektorů
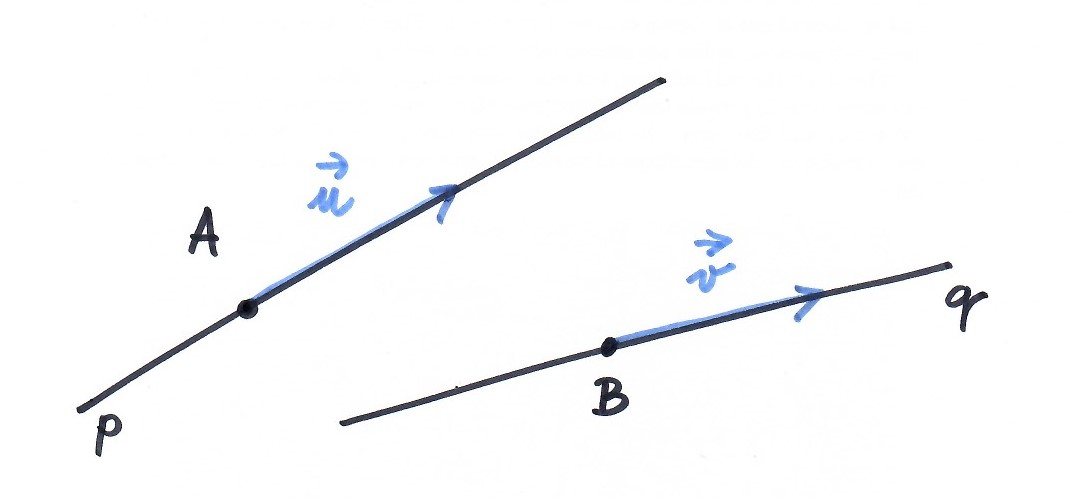
přímka $\times$ přímka
Využitím lineární závislosti vektorů
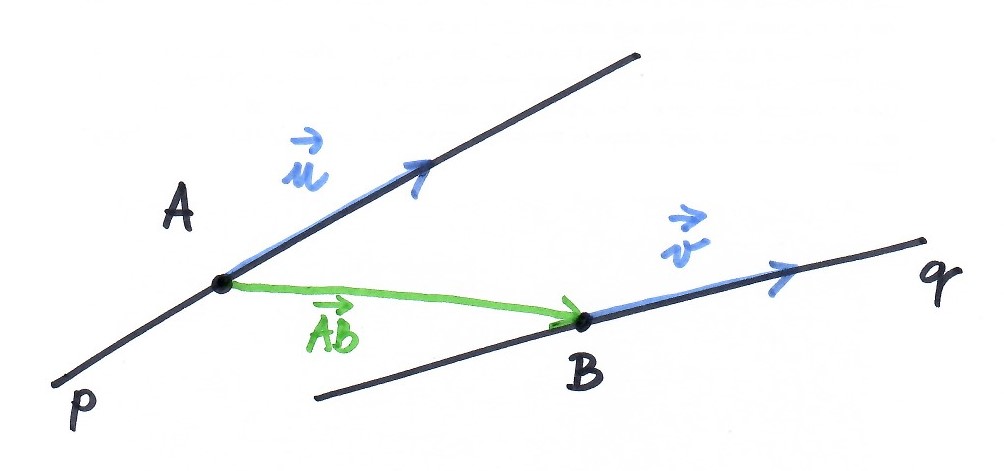
přímka $\times$ přímka
Využitím lineární závislosti vektorů
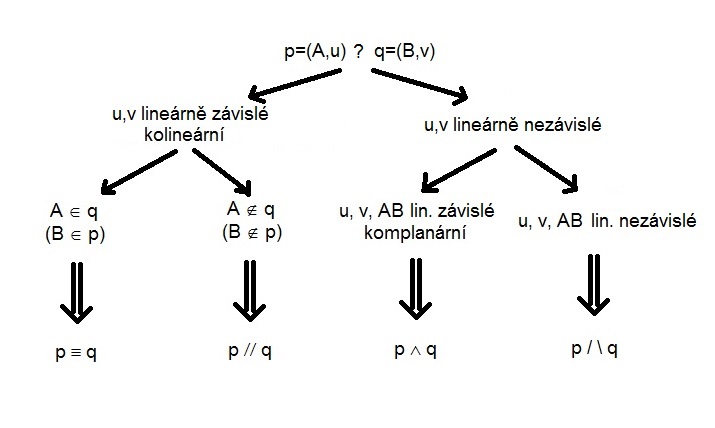
přímka $\times$ přímka
Určete vzájemnou polohu přímek $p = MN$ a $q = (K,\vec{v})$. $M = [1,-1,0], N = [2,1,1], K = [3,3,4], \vec{v} = (2,4,2).$
přímka $\times$ přímka
Řešení:
$\vec{MN}=N-M=(1,2,1)\ \text{je kolineární s}\ \vec{v}=(2,4,2)$
$\implies$ přímky jsou rovnoběžné nebo totožné
$\vec{MK}=K-M=(2,4,4)\ \text{není kolineární s}\ \vec{MN}$
$\implies$ přímky $p$, $q$ jsou rovnoběžné.
přímka $\times$ rovina
Klasicky - podle počtu řešení "soustavy rovnic" - 1 rovnice pro 1 neznámou
- nekonečně mnoho řešení (dim 1) $\Leftrightarrow$ přímka leží v rovině
- právě jedno řešení $\Leftrightarrow$ přímka různoběžná s rovinou
- žádné řešení $\Leftrightarrow$ přímka rovnoběžná s rovinou
přímka $\times$ rovina
Využitím vztahu kolmosti dvou vektorů
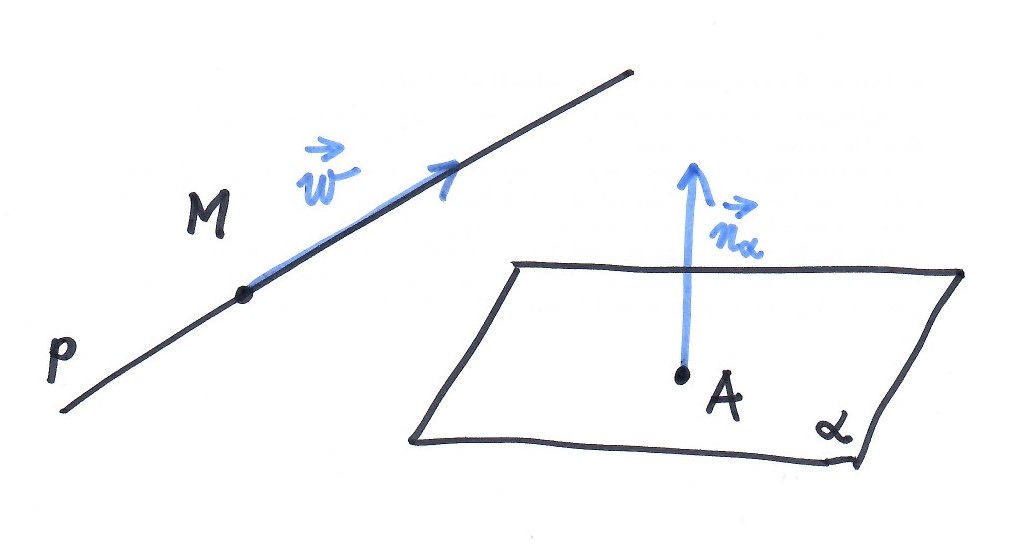
přímka $\times$ rovina
Využitím vztahu kolmosti/lin. závislosti vektorů

přímka $\times$ rovina
Využitím vztahu kolmosti/lin. závislosti vektorů
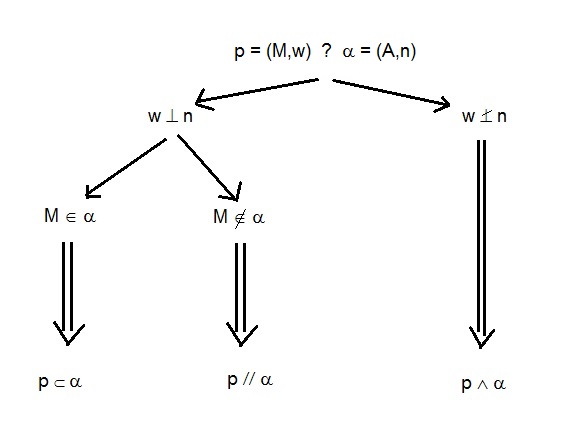
rovina $\times$ rovina
Klasicky - podle počtu řešení soustavy 2 rovnic pro 3 neznámé
- nekonečně mnoho řešení (dim=2) $\Leftrightarrow$ roviny totožné
- nekonečně mnoho řešení (dim=1) $\Leftrightarrow$ roviny různoběžné
- žádné řešení $\Leftrightarrow$ roviny rovnoběžné
rovina $\times$ rovina
Využitím lineární závislosti vektorů

rovina $\times$ rovina
Využitím lineární závislosti vektorů

rovina $\times$ rovina
Využitím lineární závislosti vektorů
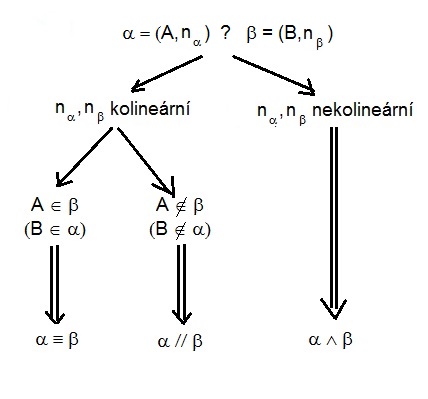
rovina $\times$ rovina
Určete vzájemnou polohu rovin $\alpha, \beta$.
$\alpha: 3x + y + z = 3$,
$\beta: x + y + 2z = 2.$
$\alpha: 3x + y + z = 3$,
$\beta: x + y + 2z = 2.$
rovina $\times$ rovina
Řešení:
$\vec{n_\alpha}=(3,1,1)$, $\vec{n_\beta}=(1,1,2)\ \text{nekolineární}$
$\implies$ roviny $\alpha, \beta$ jsou různoběžné.
rovina $\times$ rovina
Najděte společné body rovin $\alpha, \beta$.
$\alpha: 3x + y + z = 3$,
$\beta: x + y + 2z = 2.$
$\alpha: 3x + y + z = 3$,
$\beta: x + y + 2z = 2.$
rovina $\times$ rovina
Metrické úlohy v prostoru
odchylka
- dvou přímek $p = (M, \vec{u}), q = (N, \vec{v})$
\[\cos\varphi=\frac{|\vec{u}\cdot\vec{v}|}{\|\vec{u}\|\|\vec{v}\|}, \varphi\in\langle 0,\frac{\pi}{2}\rangle\] - dvou rovin $\alpha = (A, \vec{n_{\alpha}}), \beta = (B, \vec{n_{\beta}})$ \[\cos\varphi=\frac{|\vec{n_{\alpha}}\cdot\vec{n_{\beta}}|}{\|\vec{n_{\alpha}}\|\|\vec{n_{\beta}}\|}, \varphi\in\langle 0,\frac{\pi}{2}\rangle\]
- přímky $p = (M, \vec{u})$ od roviny $\alpha = (A, \vec{n_{\alpha}})$ \[\cos\varphi'=\frac{|\vec{u}\cdot\vec{n_{\alpha}}|}{\|\vec{u}\|\|\vec{n_{\alpha}}\|}, \varphi=\frac{\pi}{2}-\varphi'\]
vzdálenost, kolmost
Určete vzdálenost bodu $U$ od roviny $\rho$.
$U = [1,2,1],$ $\rho: 3x + y + 2z - 21 = 0.$
$U = [1,2,1],$ $\rho: 3x + y + 2z - 21 = 0.$