Konstruktivní geometrie
2024/25
Mgr. Marta Hlavová
marta.hlavova@fs.cvut.cz
čtvrtek 10:00 - 11:30
KN:D-304
čtvrtek 10:00 - 11:30
KN:D-304
informace o předmětu → mat.fs.cvut.cz
- obsah přednášek a cvičení
- podrobný harmonogram přednášek a cvičení
- literatura:
- přednášky RNDr. Petra Mertla:
- kopie skript Konstruktivní geometrie (po kapitolách)
- elektronická skripta Aplikovaná geometrie
- předlohy na cvičení (+ výsledky)
- požadavky k zápočtu (4 samostatné práce + ... )
- požadavky ke zkoušce (písemná, 6 příkladů za celkem 100 bodů na 120 minut)
- vzory písemky
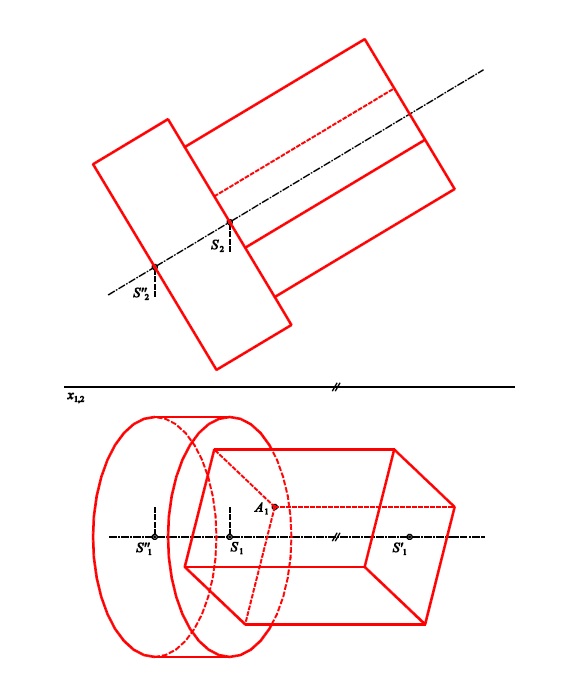
Konstruktivní geometrie 2024/25
Kinematická geometrie
v rovině
Kinematická geometrie v rovině
zabývá se chováním křivek vzniklých rovinným pohybem
Rovinná křivka - základní pojmy
- tzv. jednoparametrická množina bodů, $P(t)=[x(t),y(t)]$,
kde $x(t)$ a $y(t)$ jsou spojité funkce na intervalu $I\subset \mathbb{R}$ - tečný vektor v "rozumném" bodě křivky, $X'(t)=(x'(t),y'(t))\neq (0,0)$
- tečna
- normála
- elementární rovinné křivky: kružnice, přímka
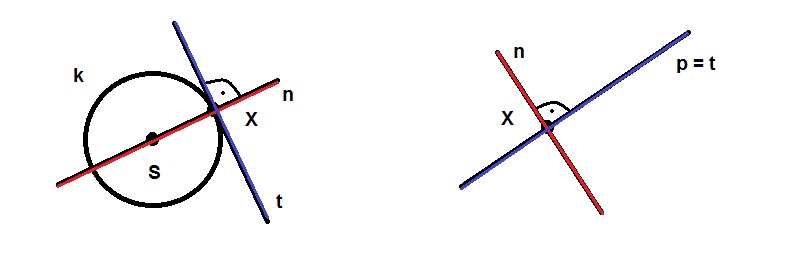
Rovinná křivka - výjimečné body
- body křivky s problematickými tečnami
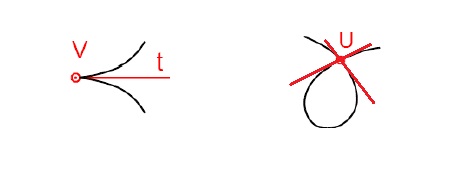
- bod vratu V - neexistuje tečný vektor, tečna dodefinovaná
- uzlový bod U - dva různé tečné vektory, dvě tečny
Rovinné křivky - dotyk
Dvě rovinné křivky se dotýkají, pokud mají v bodě dotyku společnou tečnu a normálu.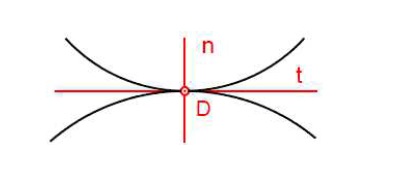
Kinematická geometrie - pohyb
Kinematická geometrie - pohyb
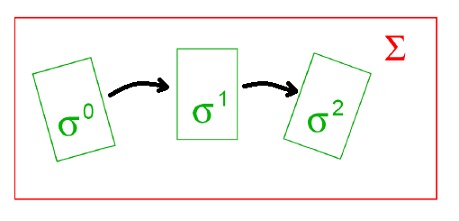
- 2 neměnné rovinné soustavy:
- pevná soustava Σ
- hybná soustava σ
- pohyb = pohyb hybné soustavy σ po pevné soustavě Σ
Křivky vzniklé rovinným pohybem
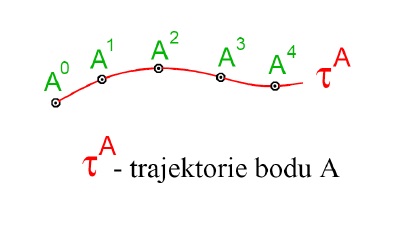
trajektorie bodu
- křivka vytvořená pohybem bodu $A$
- tzv. stopa bodu
- značení: $\tau^A$
- fáze pohybu bodu $A$ → horní index
Křivky vzniklé rovinným pohybem
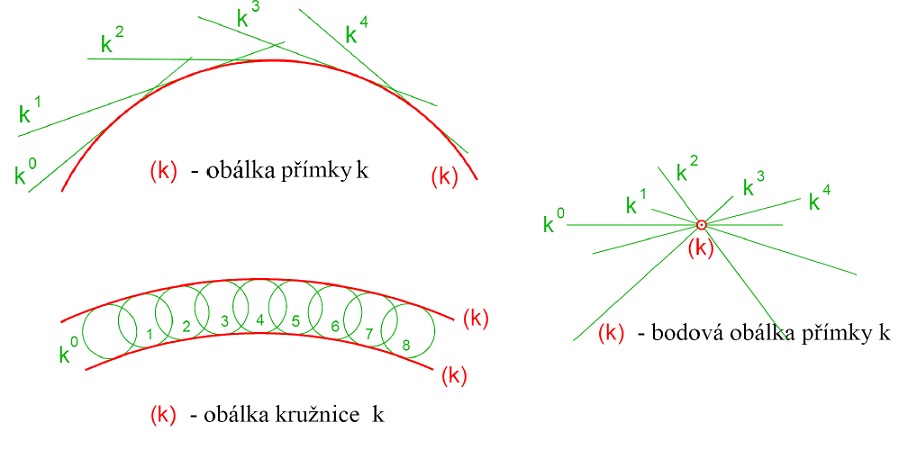
obálka křivky $k$
- křivka vytvořená pohybem křivky k
- v každém okamžiku pohybu se dotýká pohybující se křivky $k$
- značení: $(k)$
Další křivky technické praxe (*)
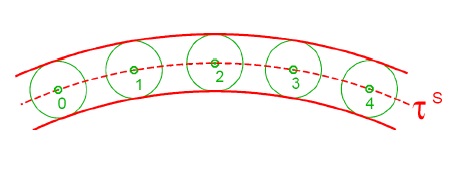
ekvidistanta křivky $k$
- křivka tvořená body v konstantní vzdálenosti od křivky $k$, kdy vzdálenost je měřena na normálách křivky $k$
Další křivky technické praxe (*)
evoluta křivky $k$
- obálka normál křivky $k$
- $l$ je evolutou křivky $k$ ↔ $k$ je tzv. evolventou křivky $l$
evoluta elipsy → asteroida
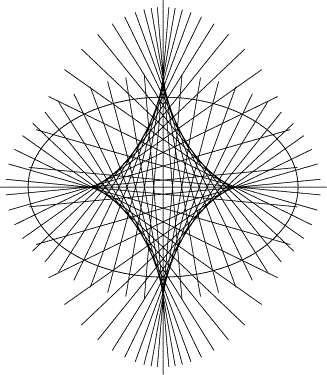
elipsa → evolventa asteroidy
Určení pohybu - I/A
- 2 body $A, B$ + jejich trajektorie $\tau^A, \tau^B$
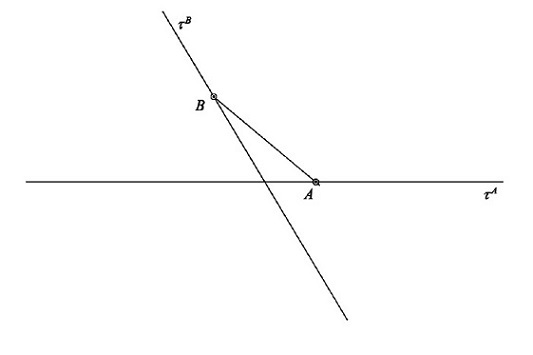
$\tau^A, \tau^B$ přímky → eliptický pohyb
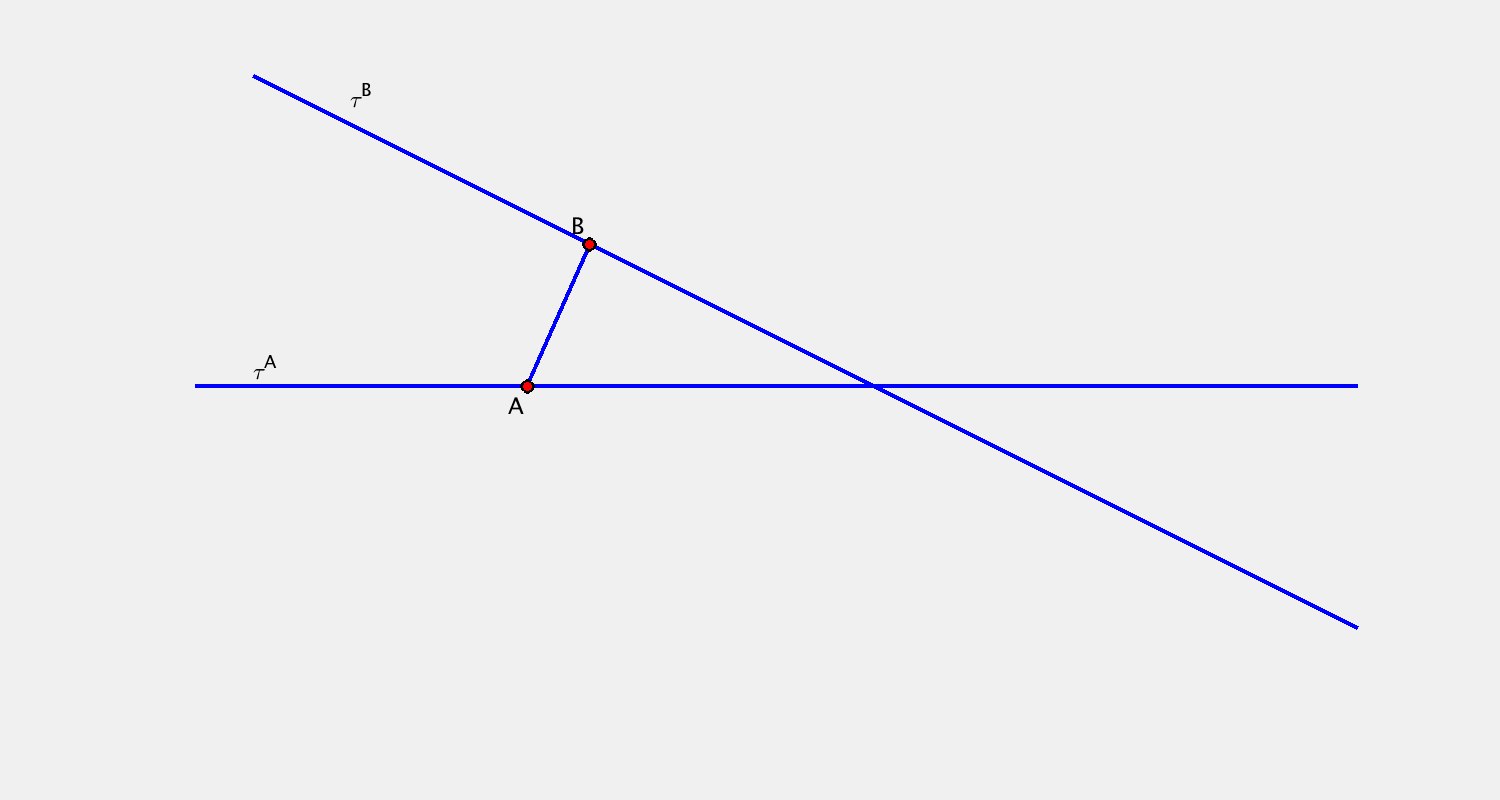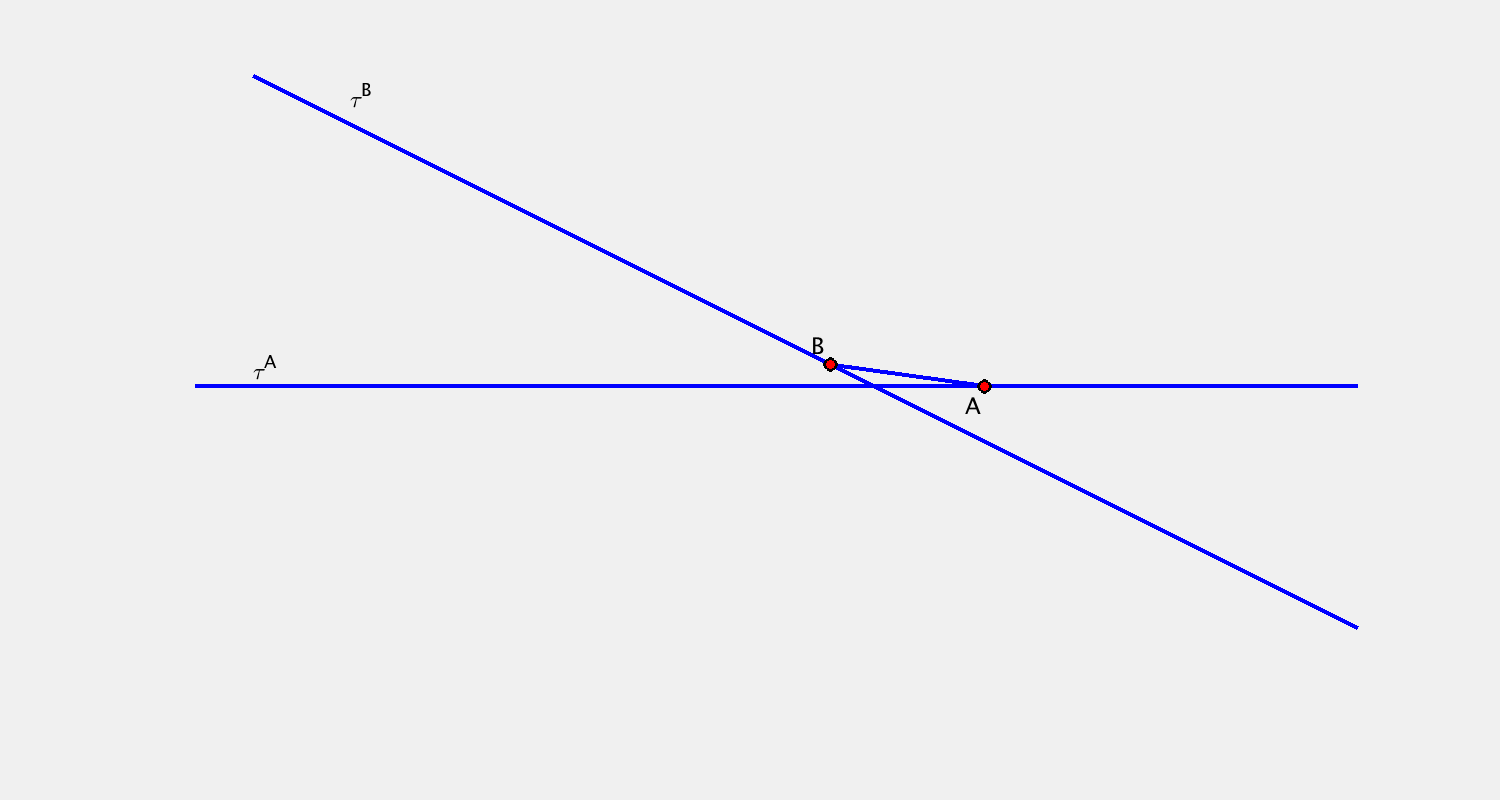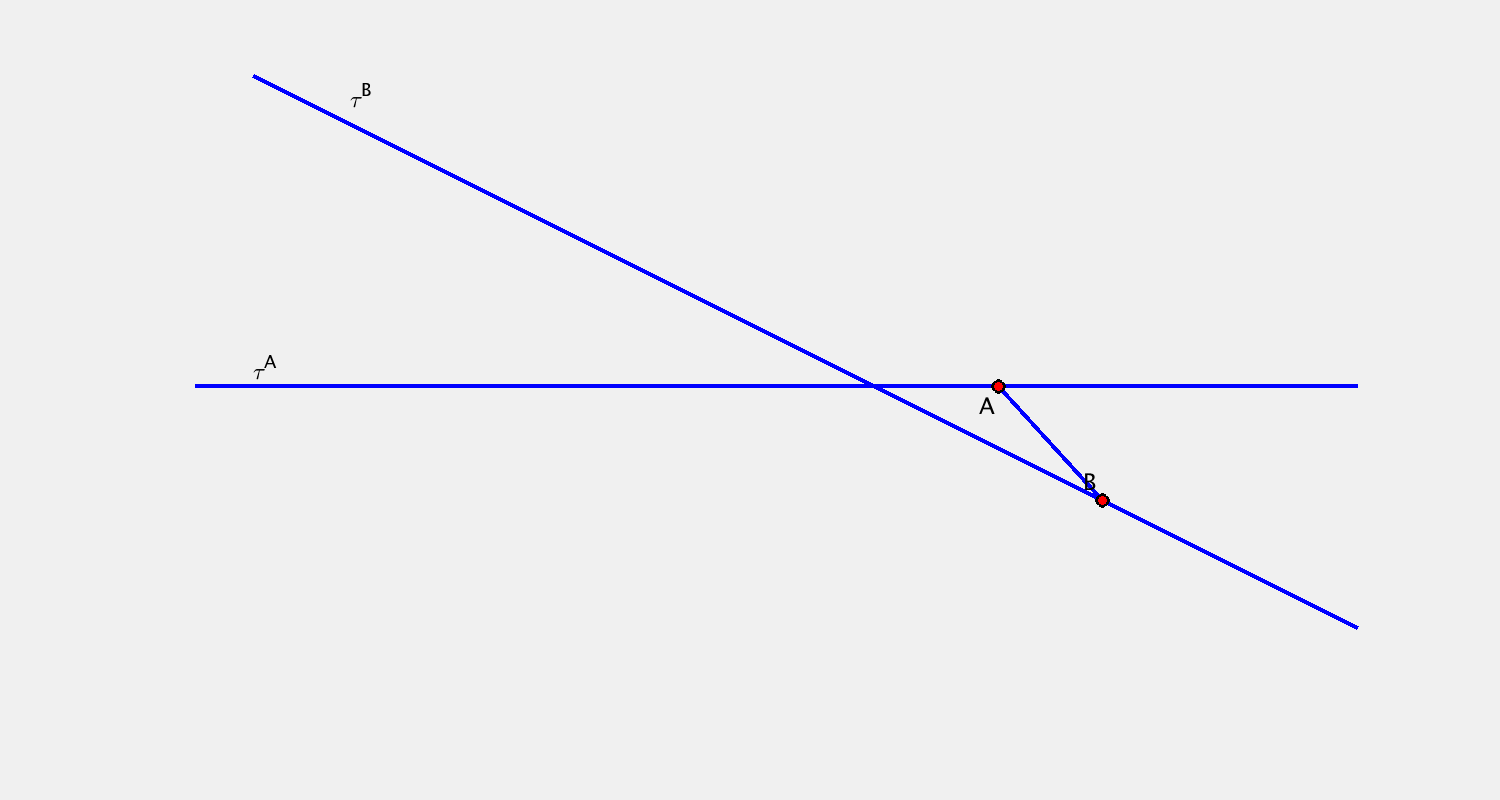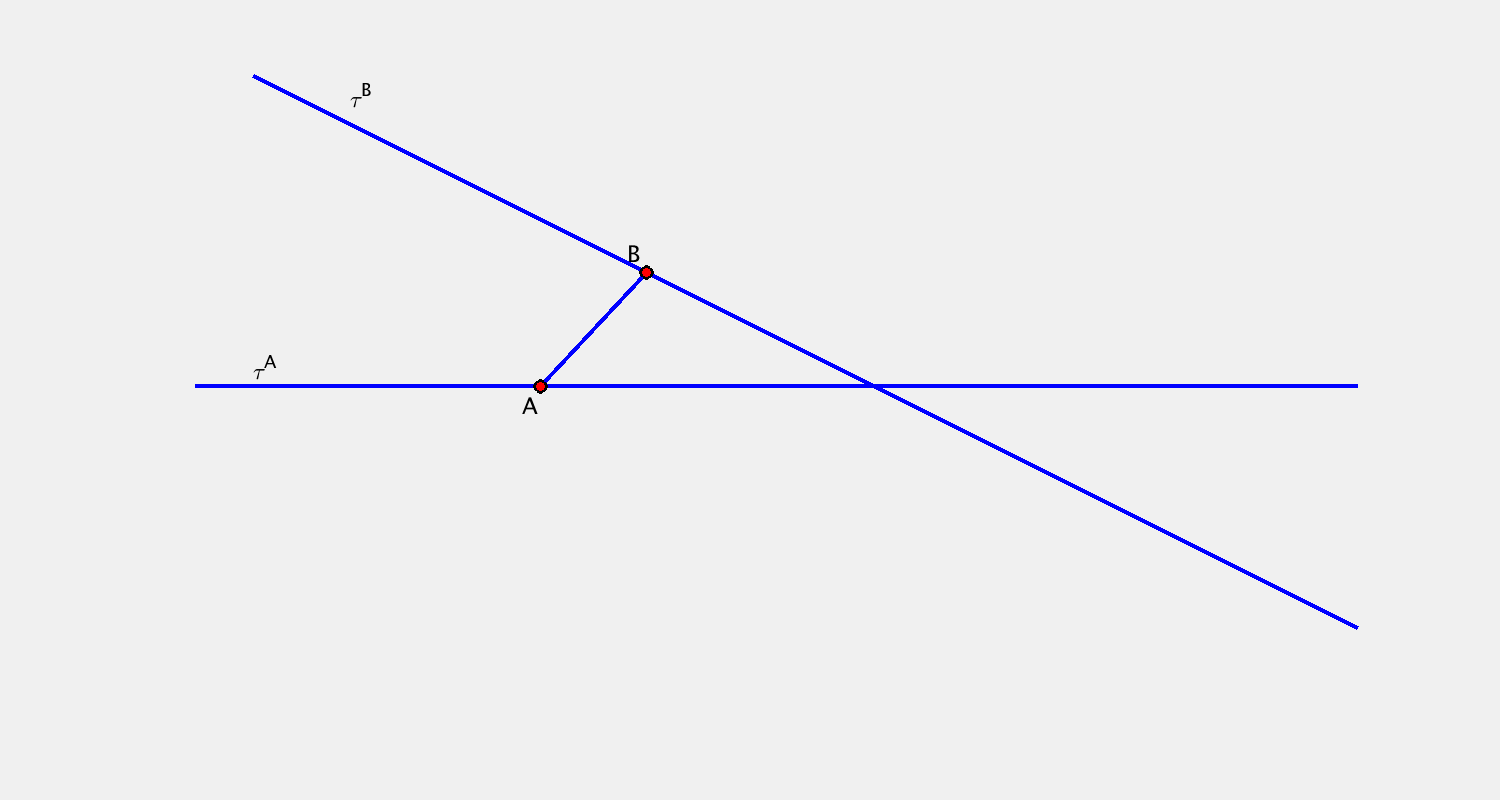
Příklad A
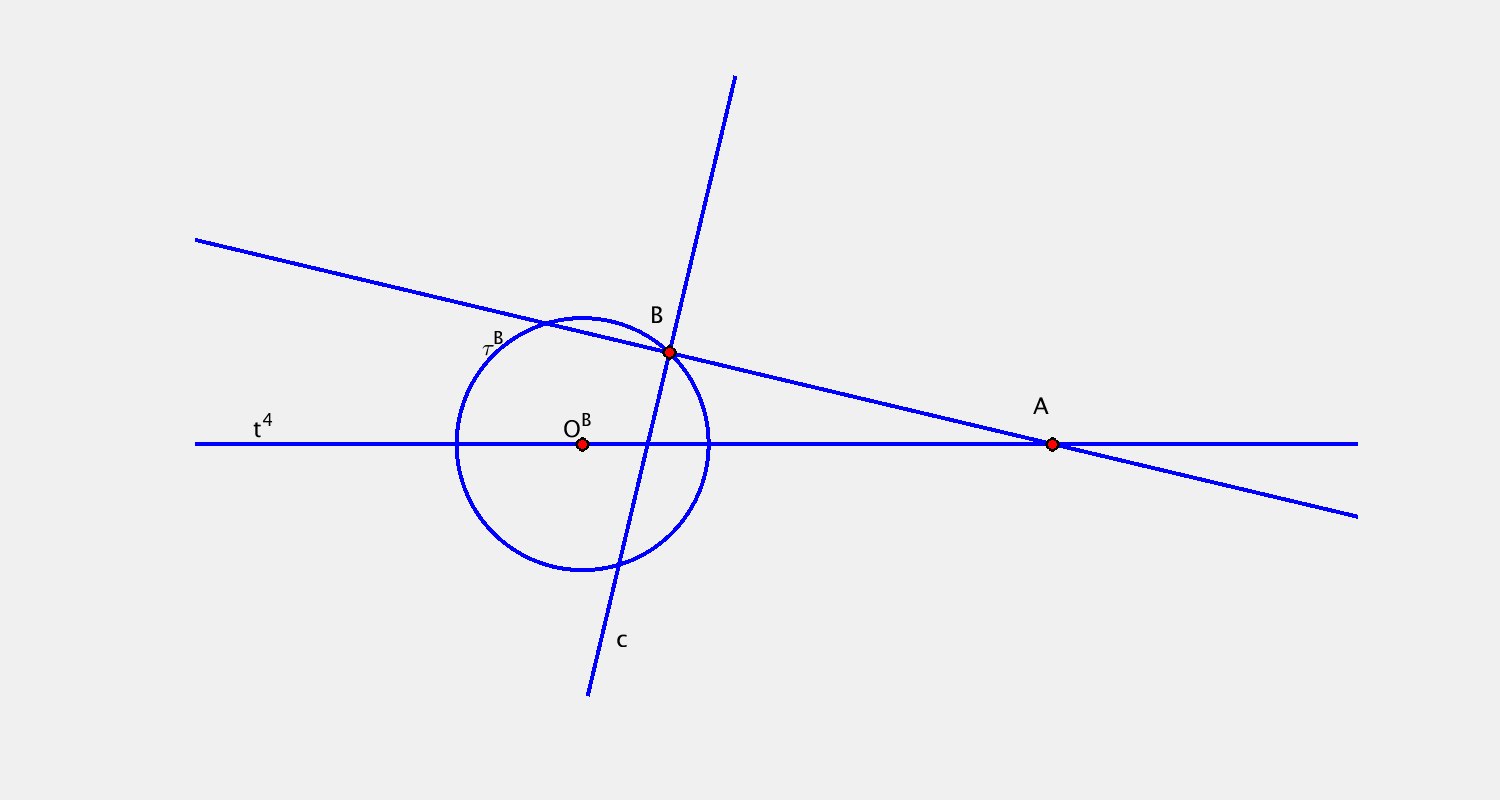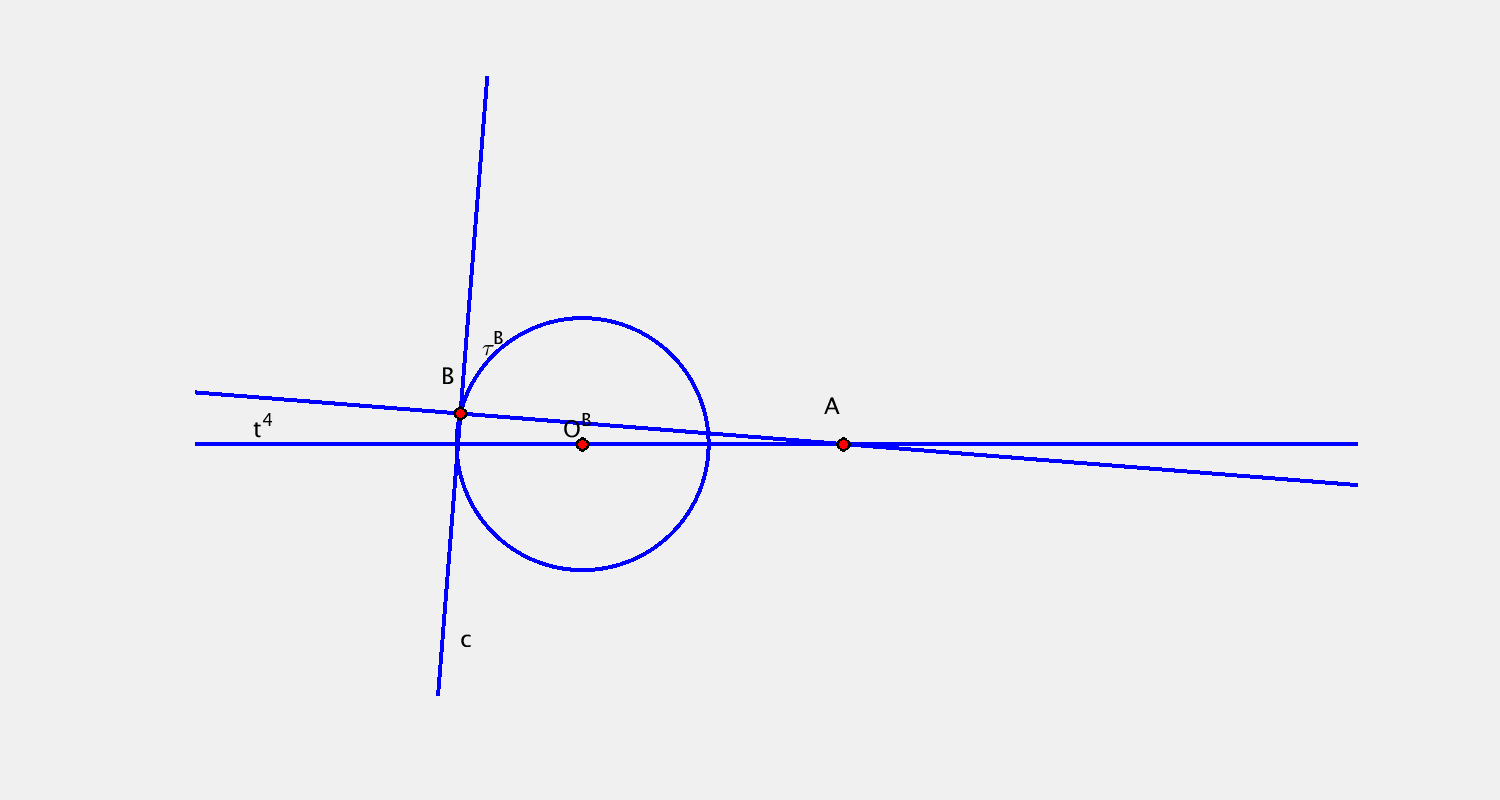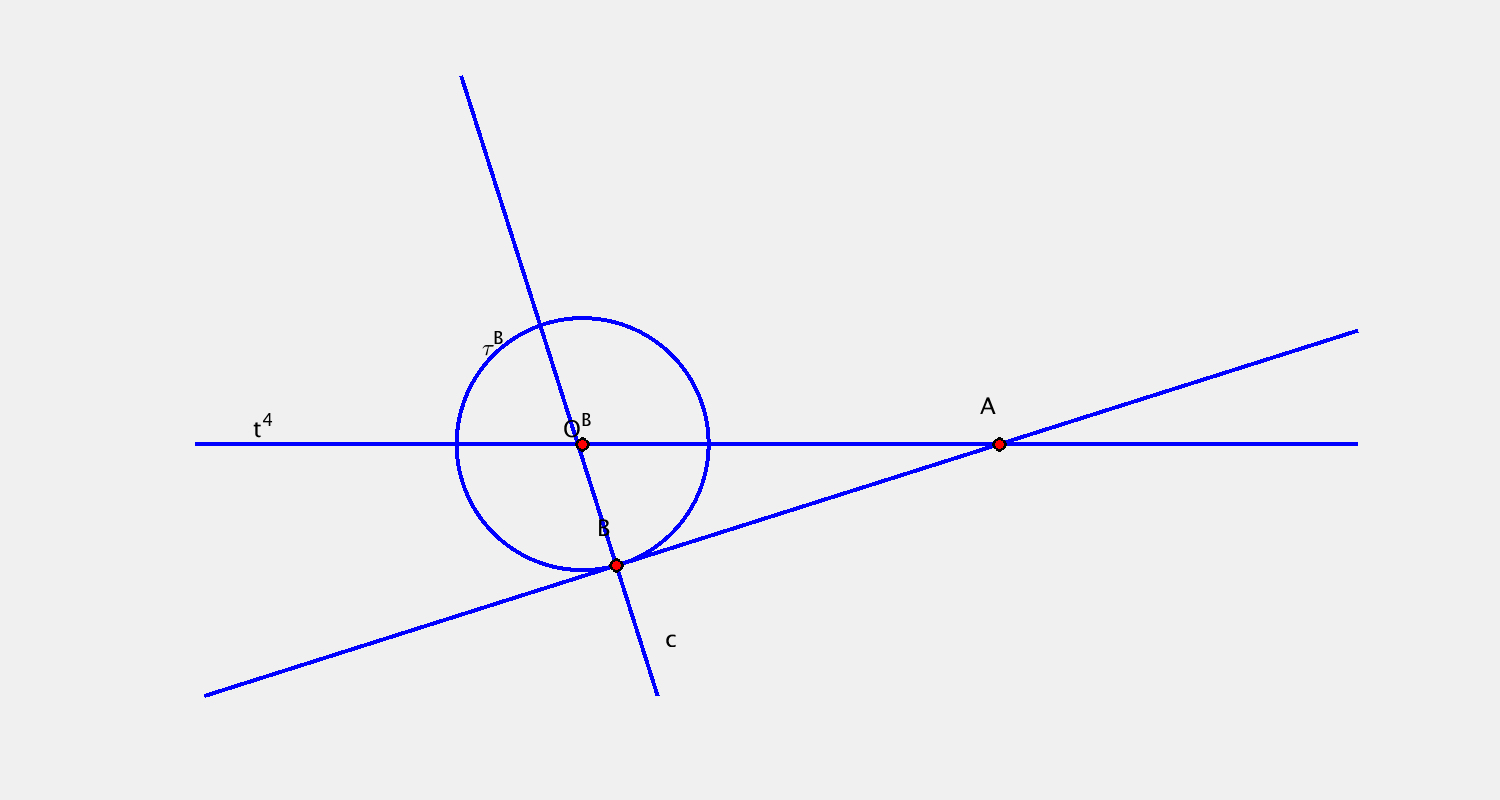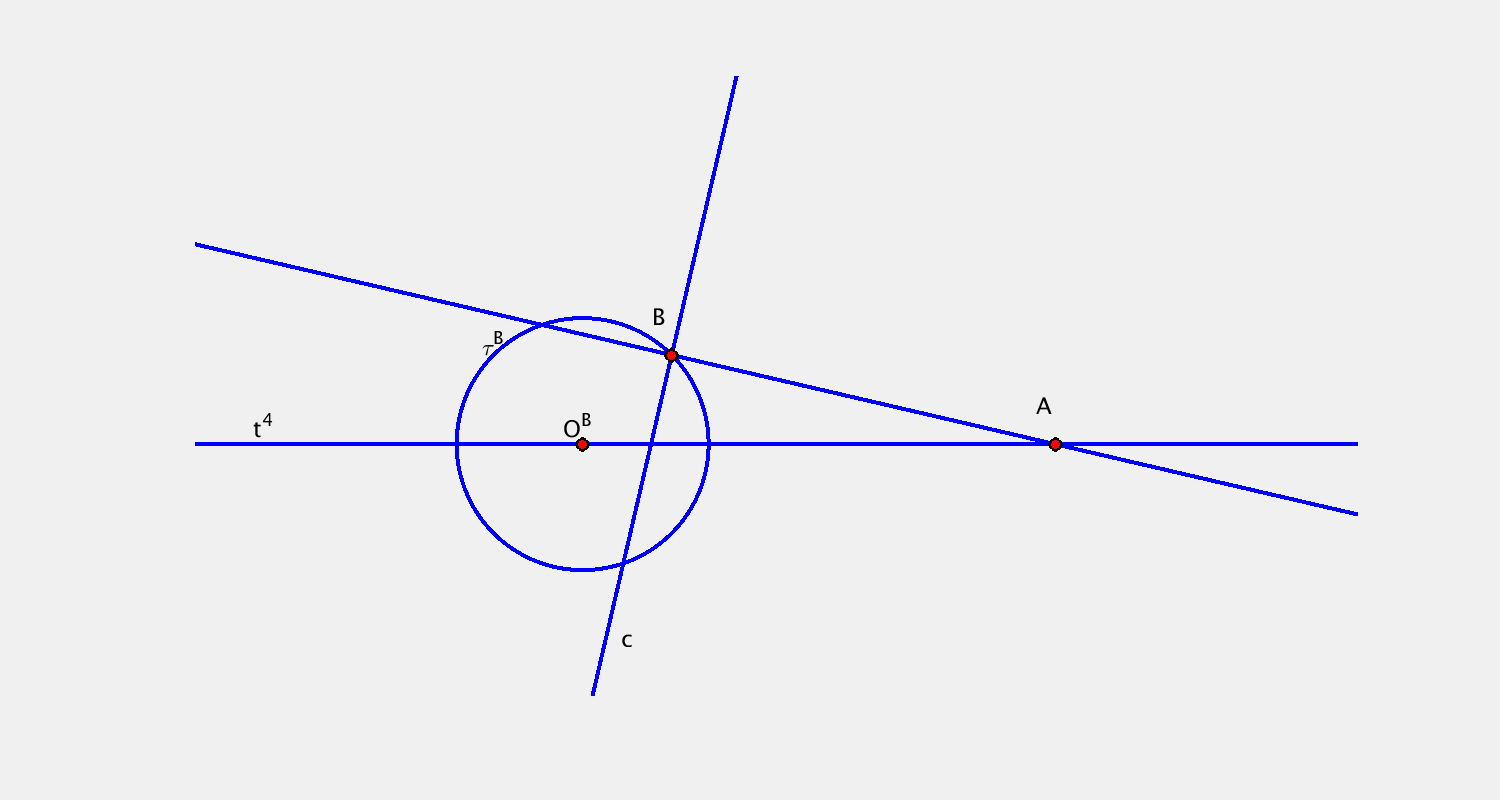
Pohyb je určen určen trajektorií bodu $A$ a trajektorií bodu $B$. Sestrojte další dvě polohy přímky $c$.
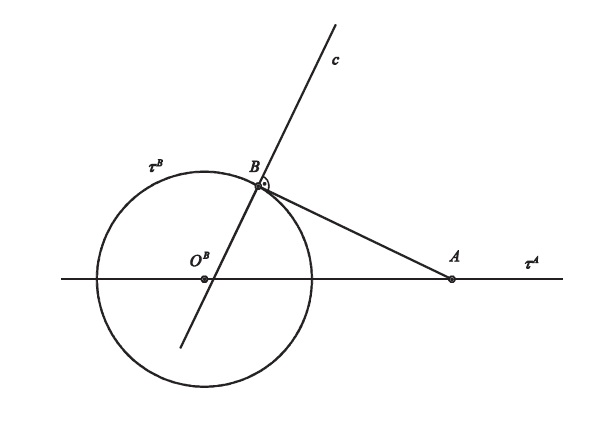
Určení pohybu - I/B
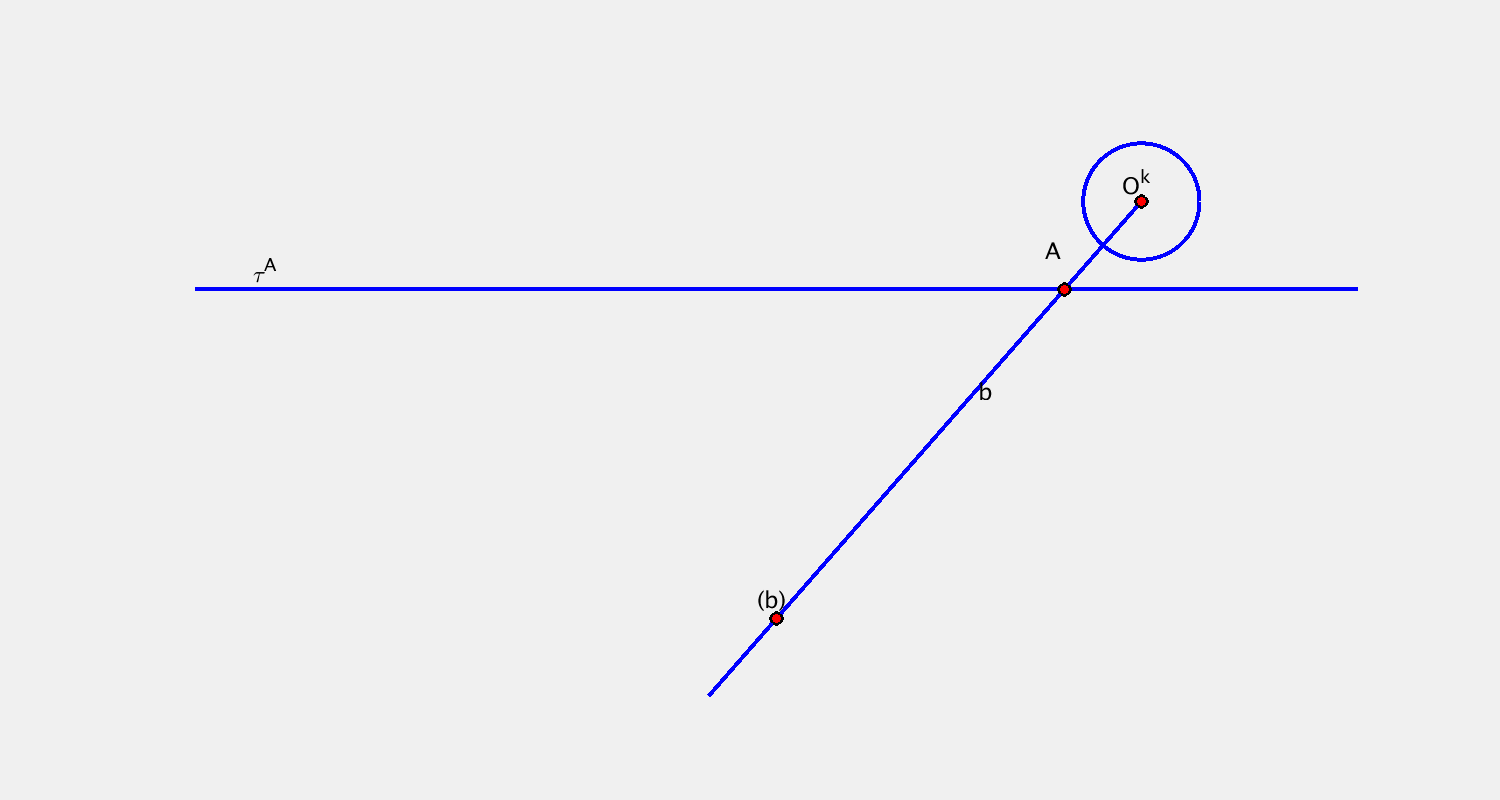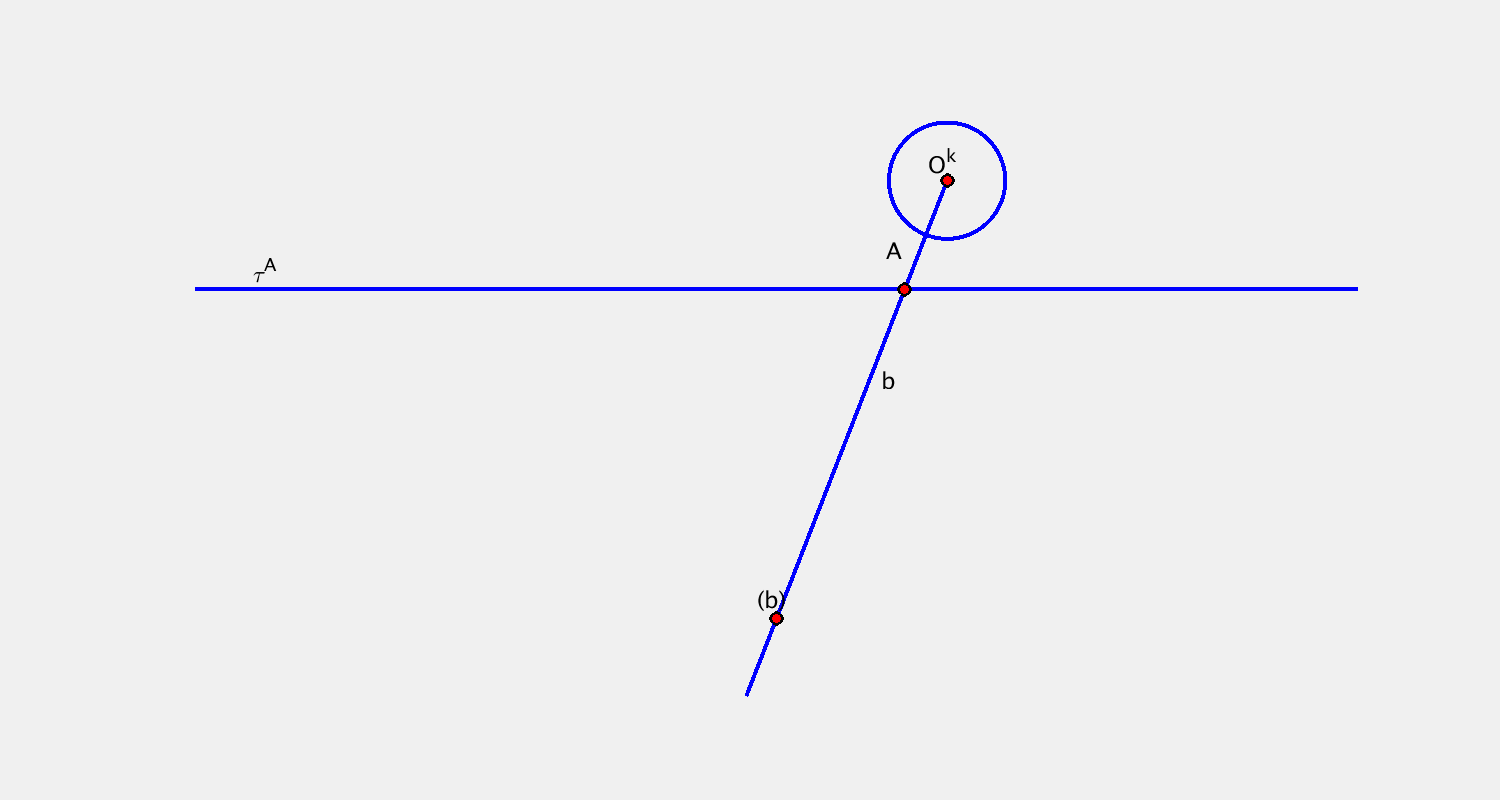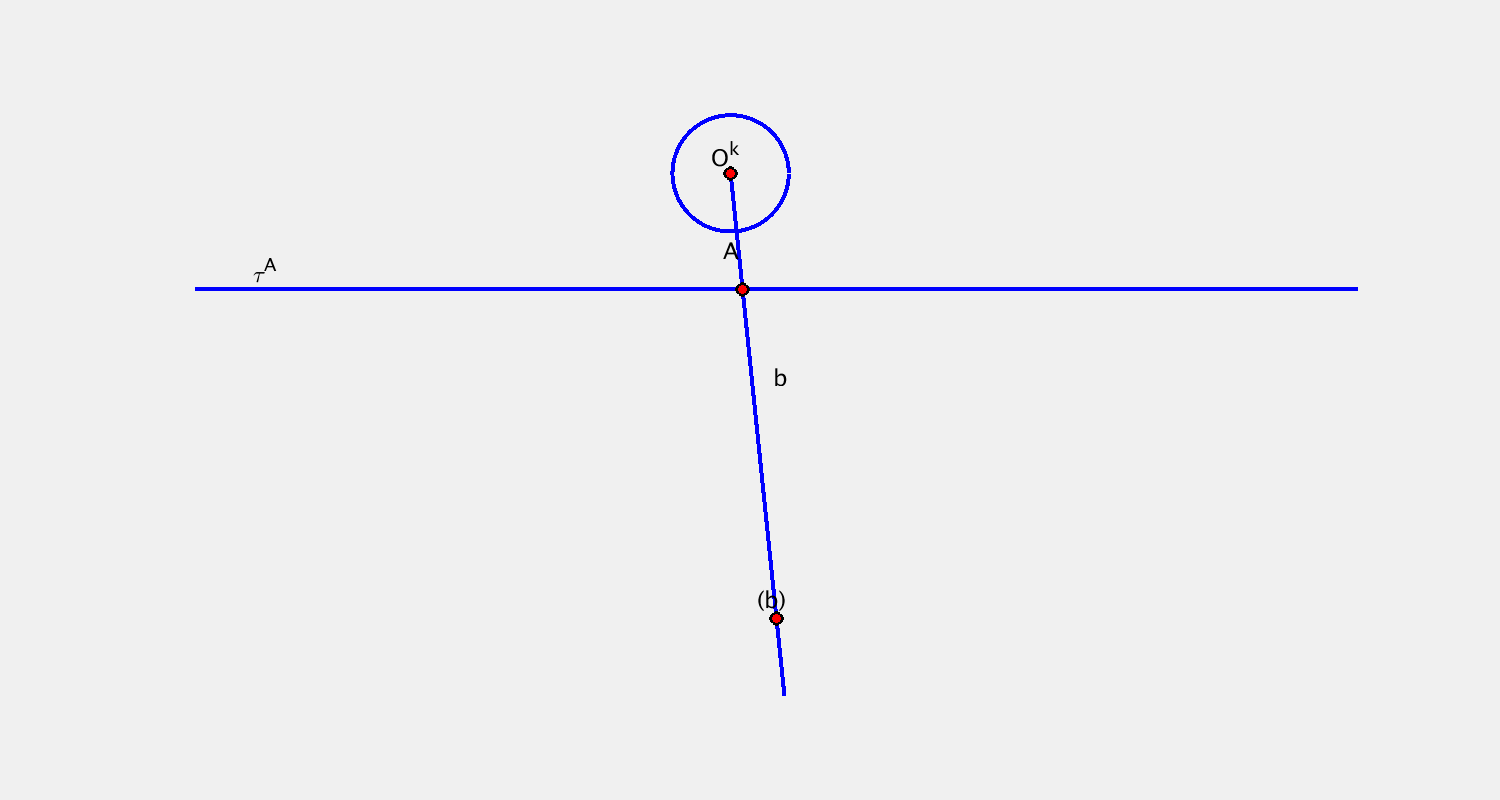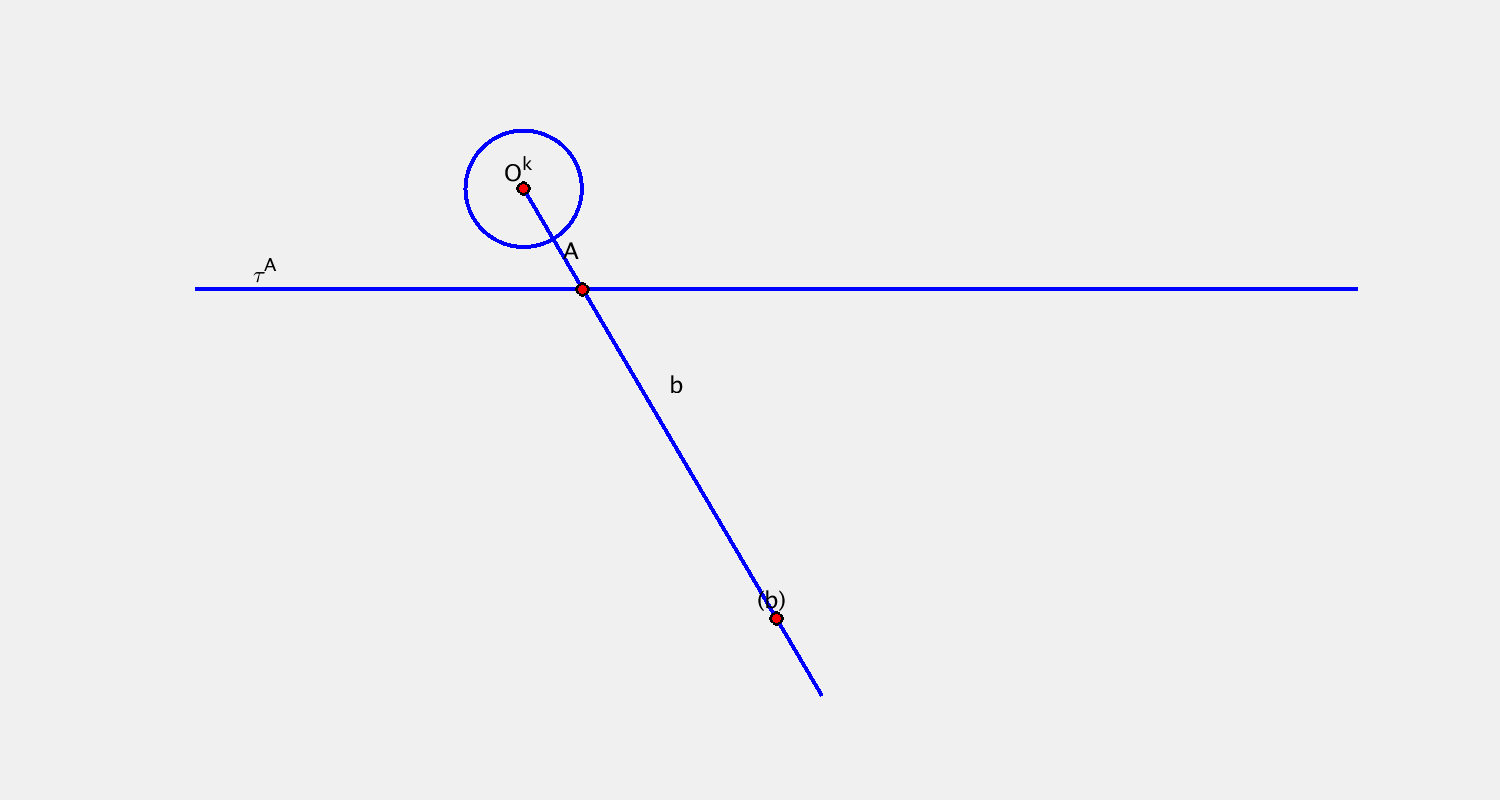
- bod $A$, křivka $b$ + trajektorie $\tau^A$, obálka $(b)$

$(b)$ bod → konchoidální pohyb
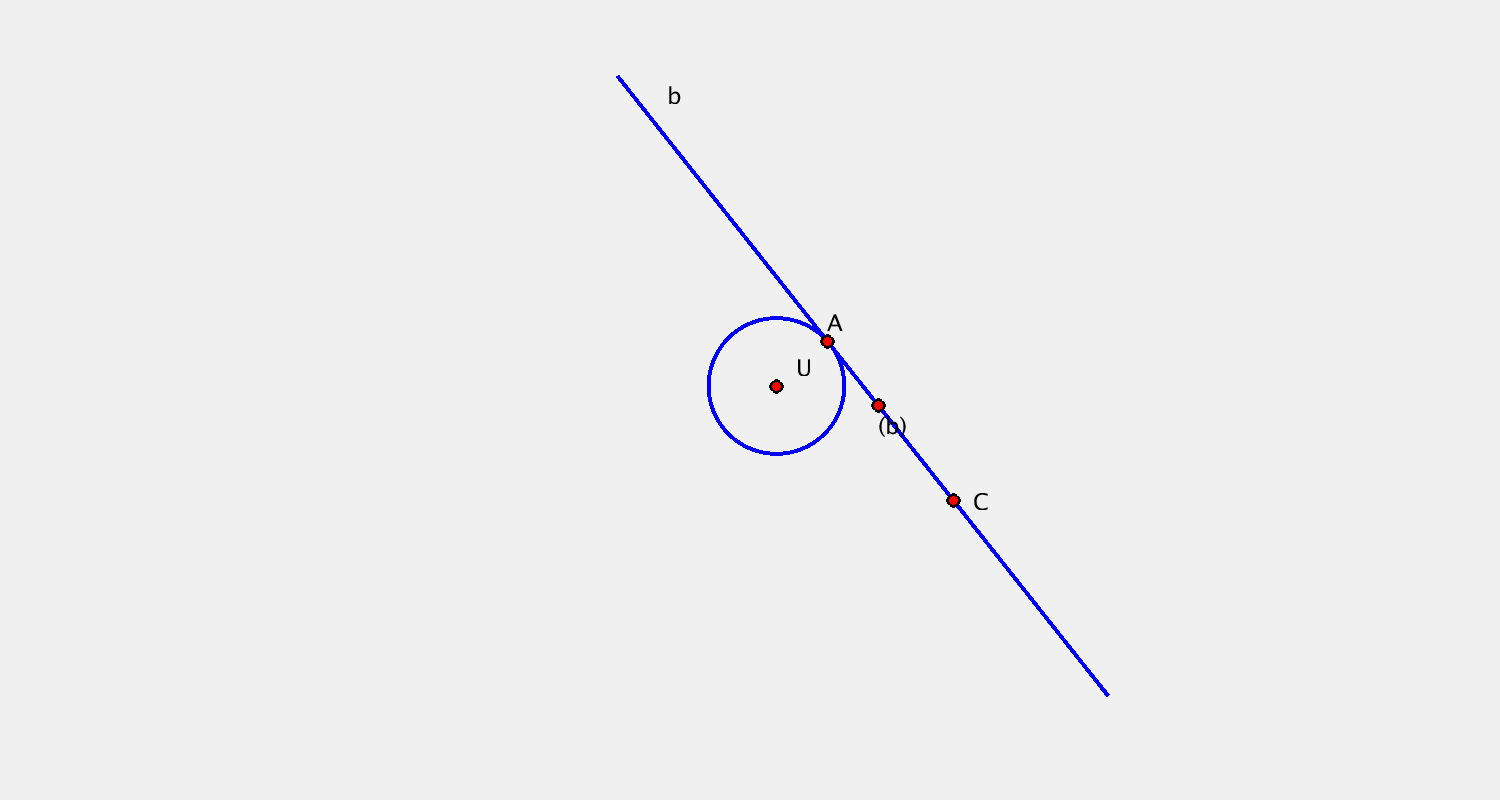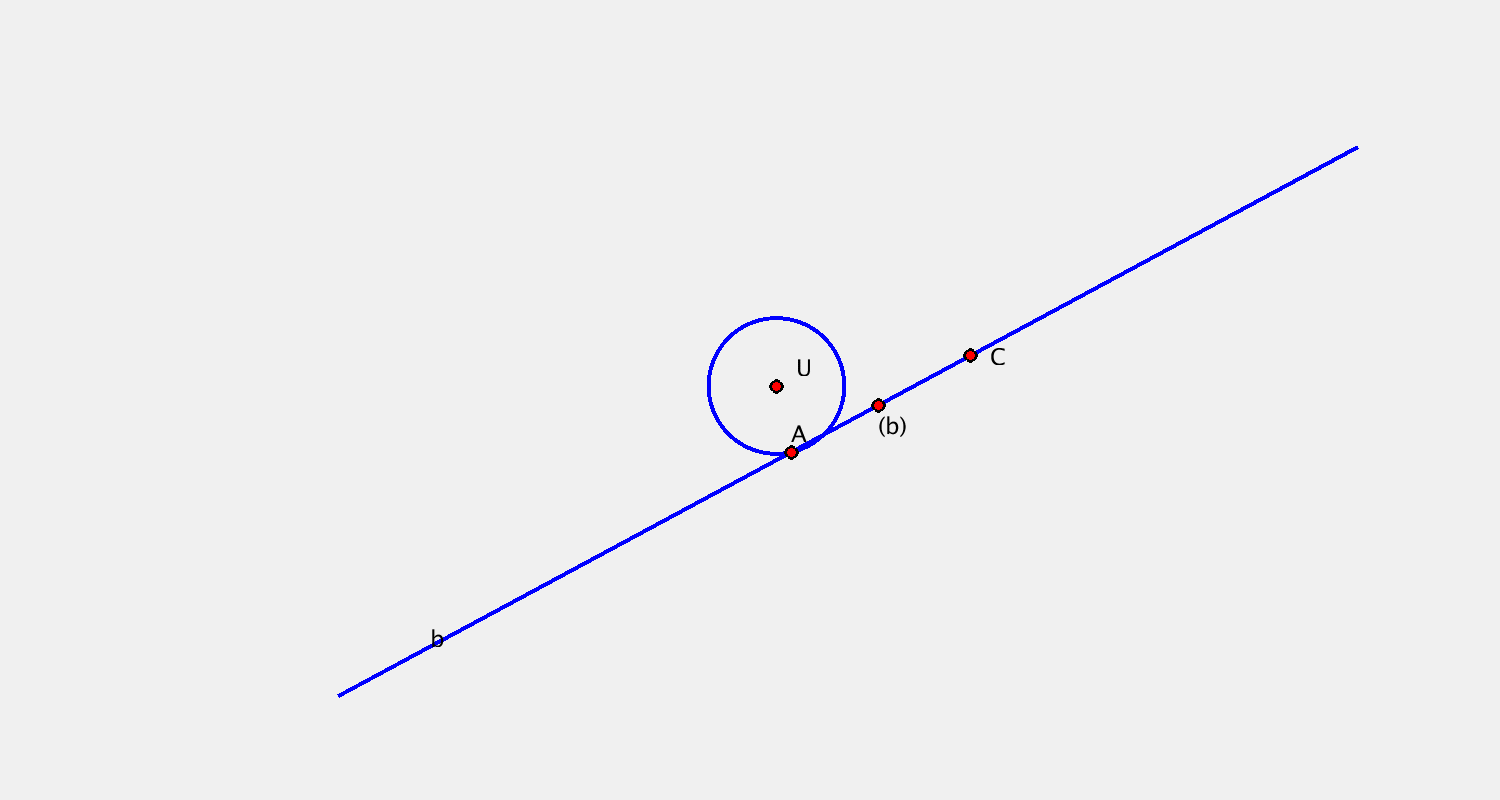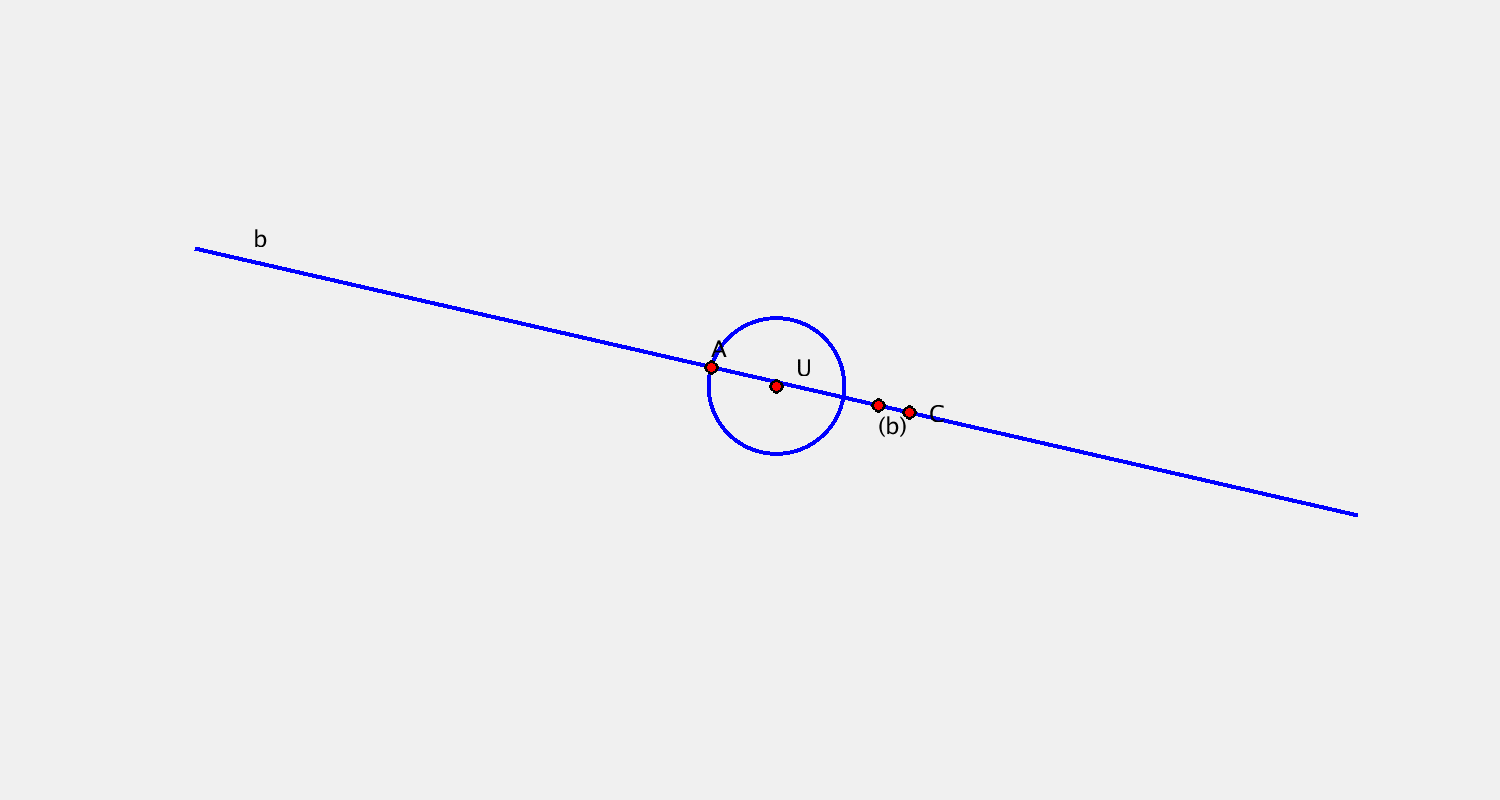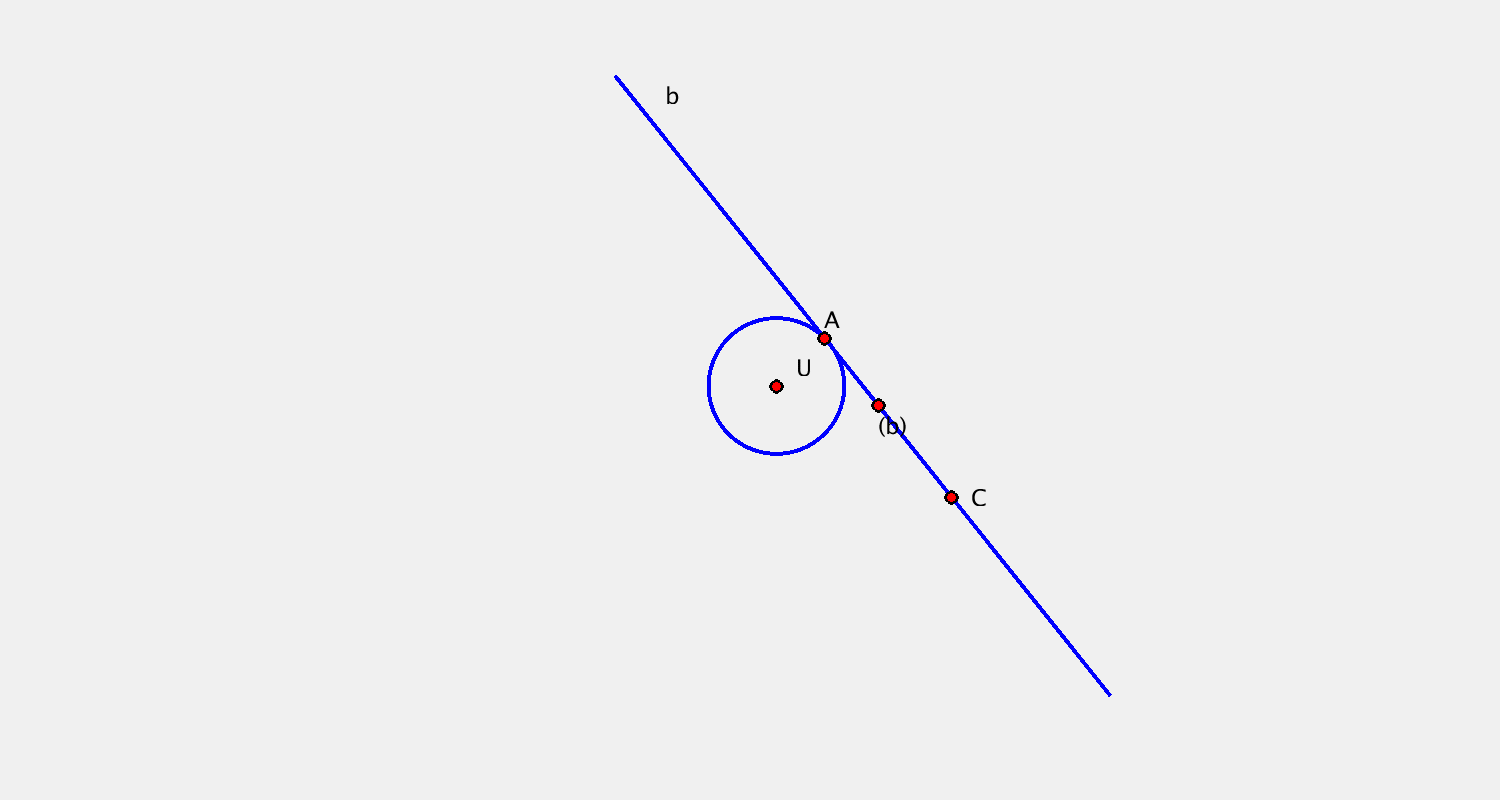
Příklad B
Pohyb je určen určen trajektorií bodu $A$ a bodovou obálkou přímky $b$. Sestrojte další dvě polohy kružnice $k$.
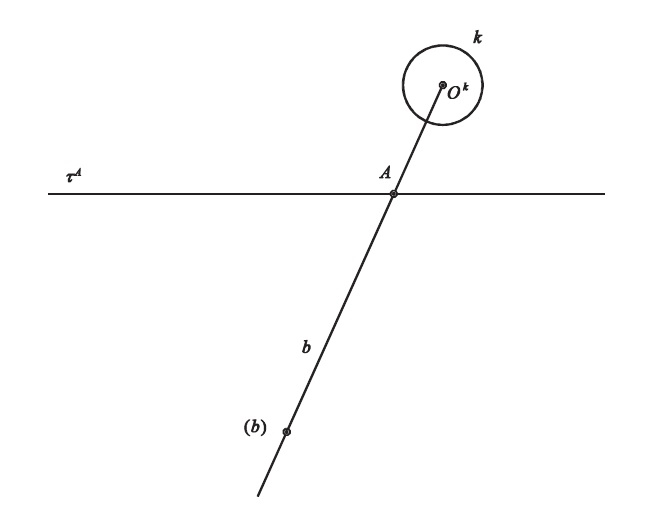
Určení pohybu - I/C
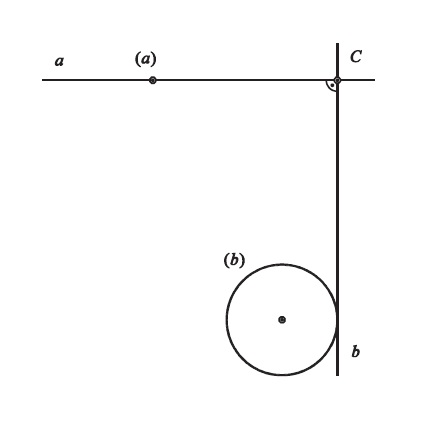
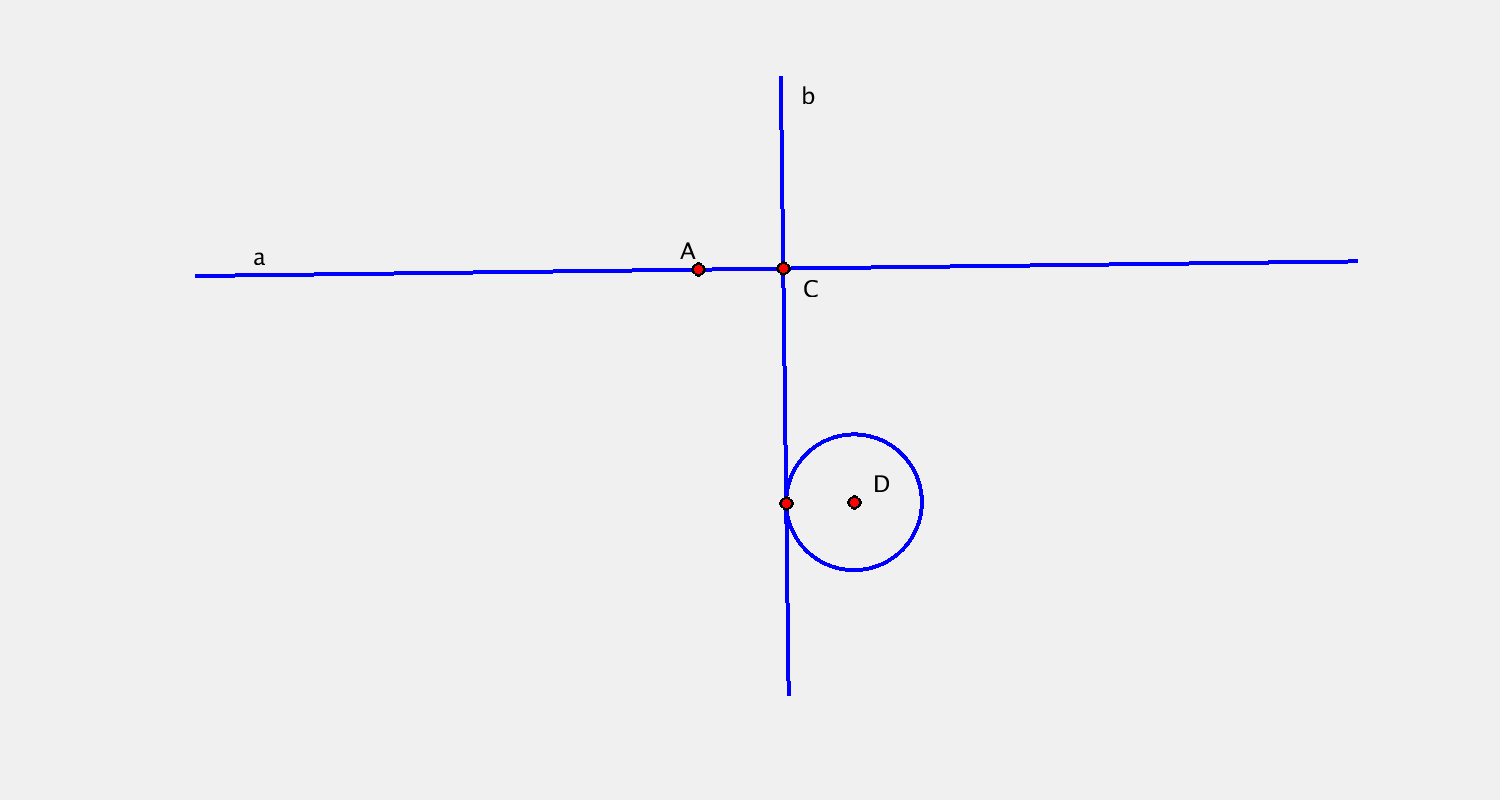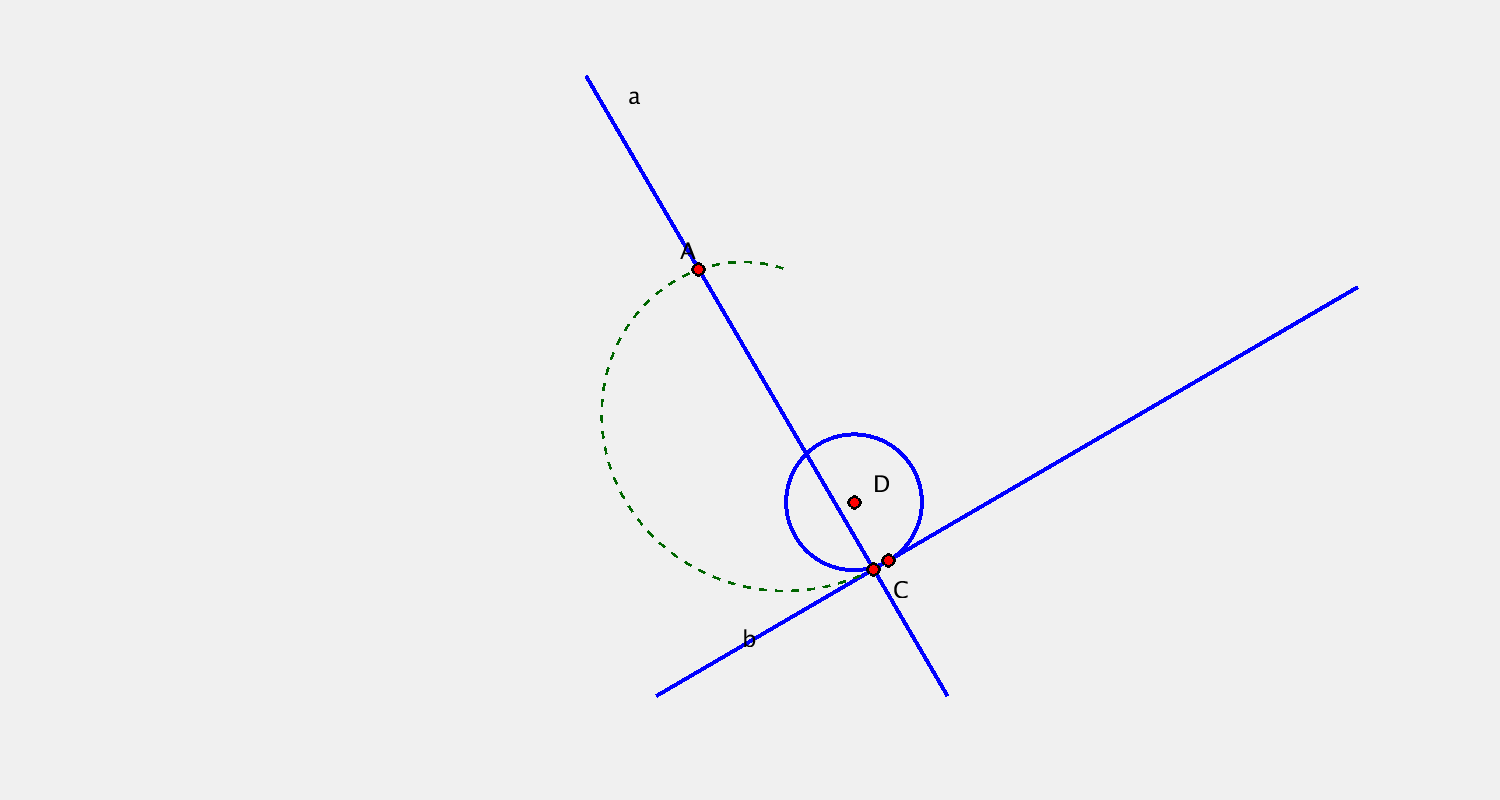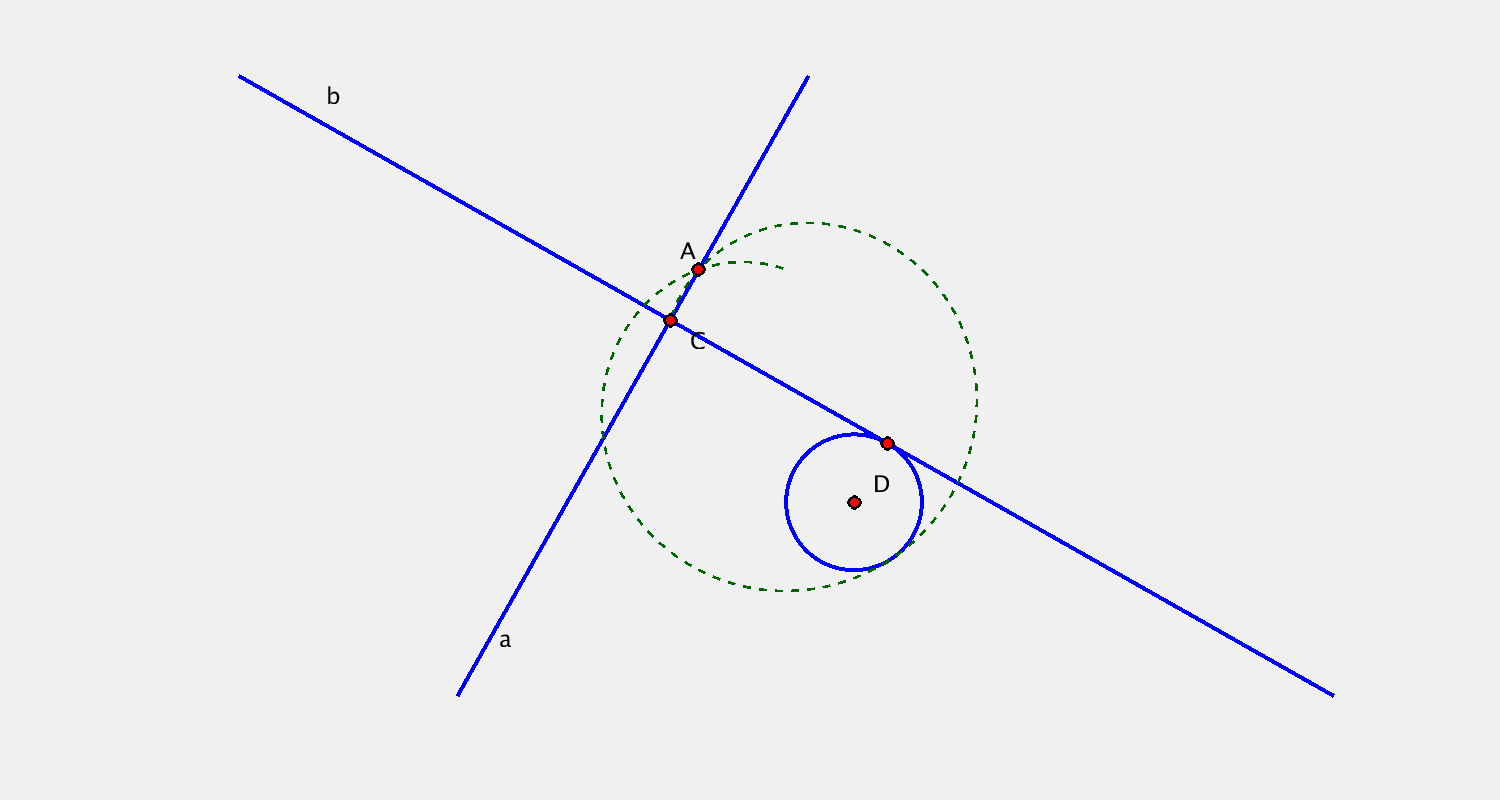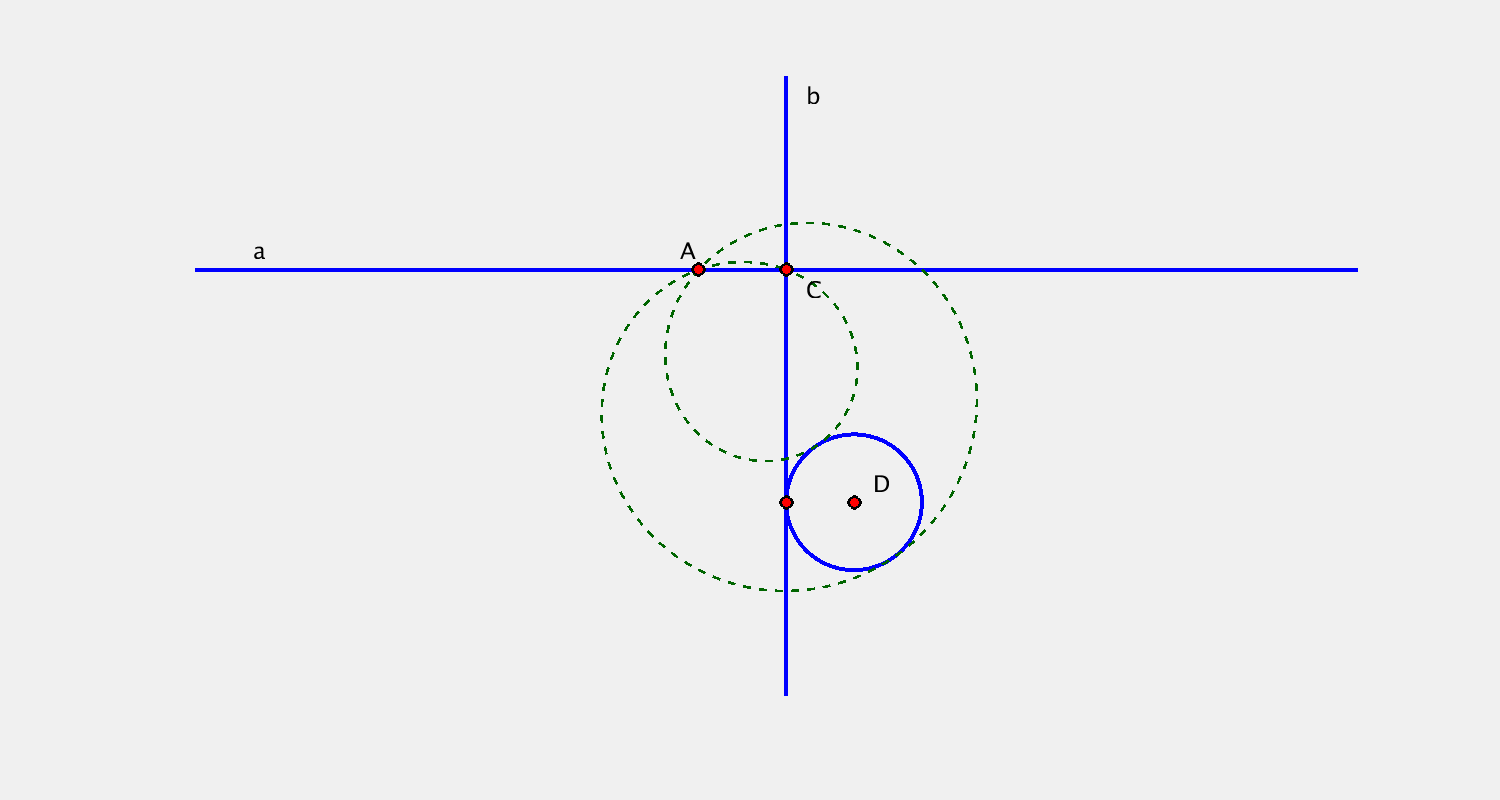
- 2 křivky $a, b$ + jejich obálky $(a), (b)$
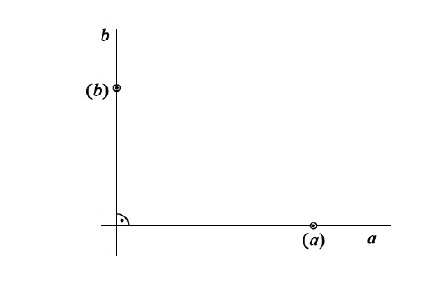
$a, b$ přímky + $(a), (b)$ body → kardioidický pohyb
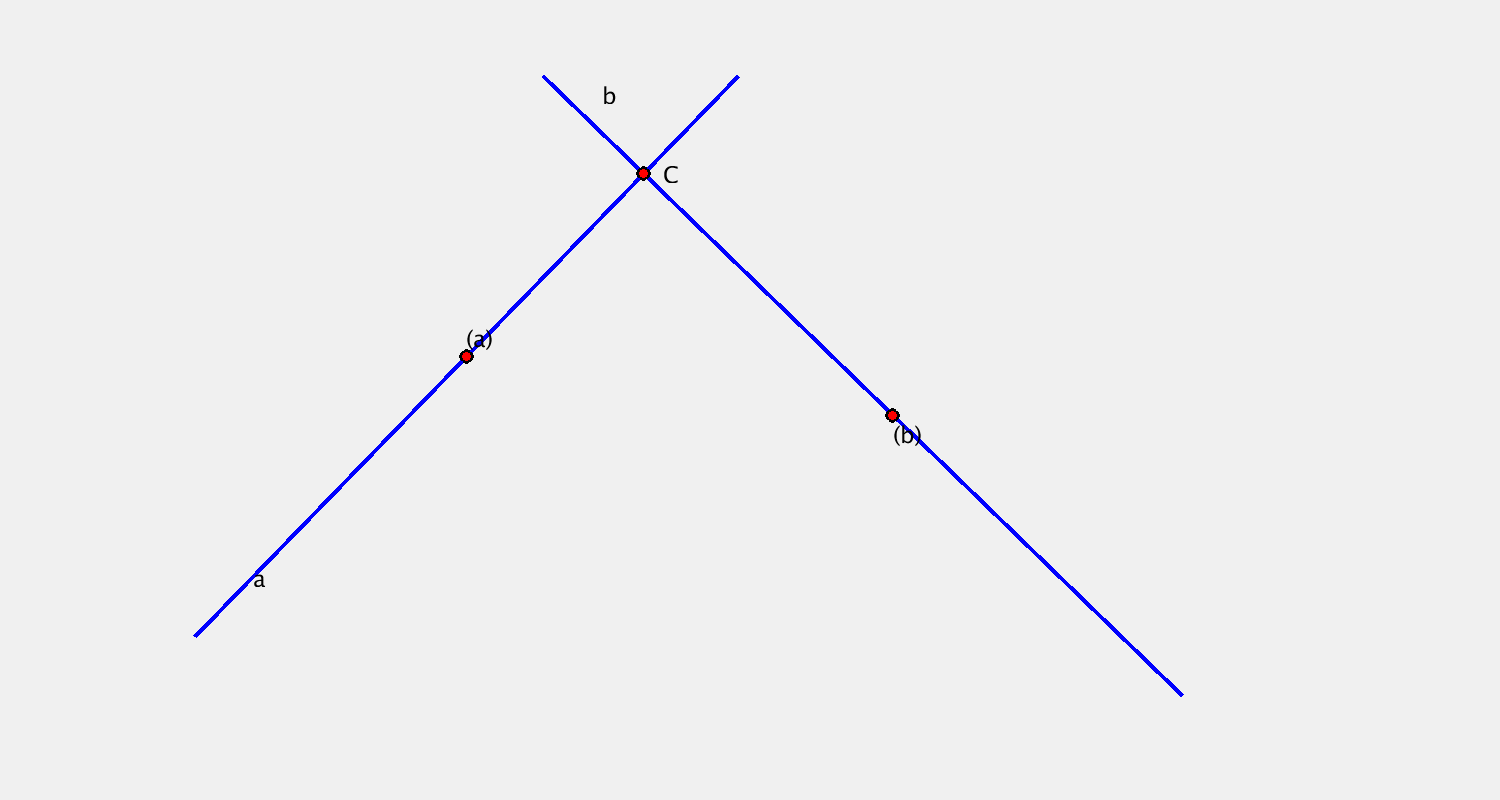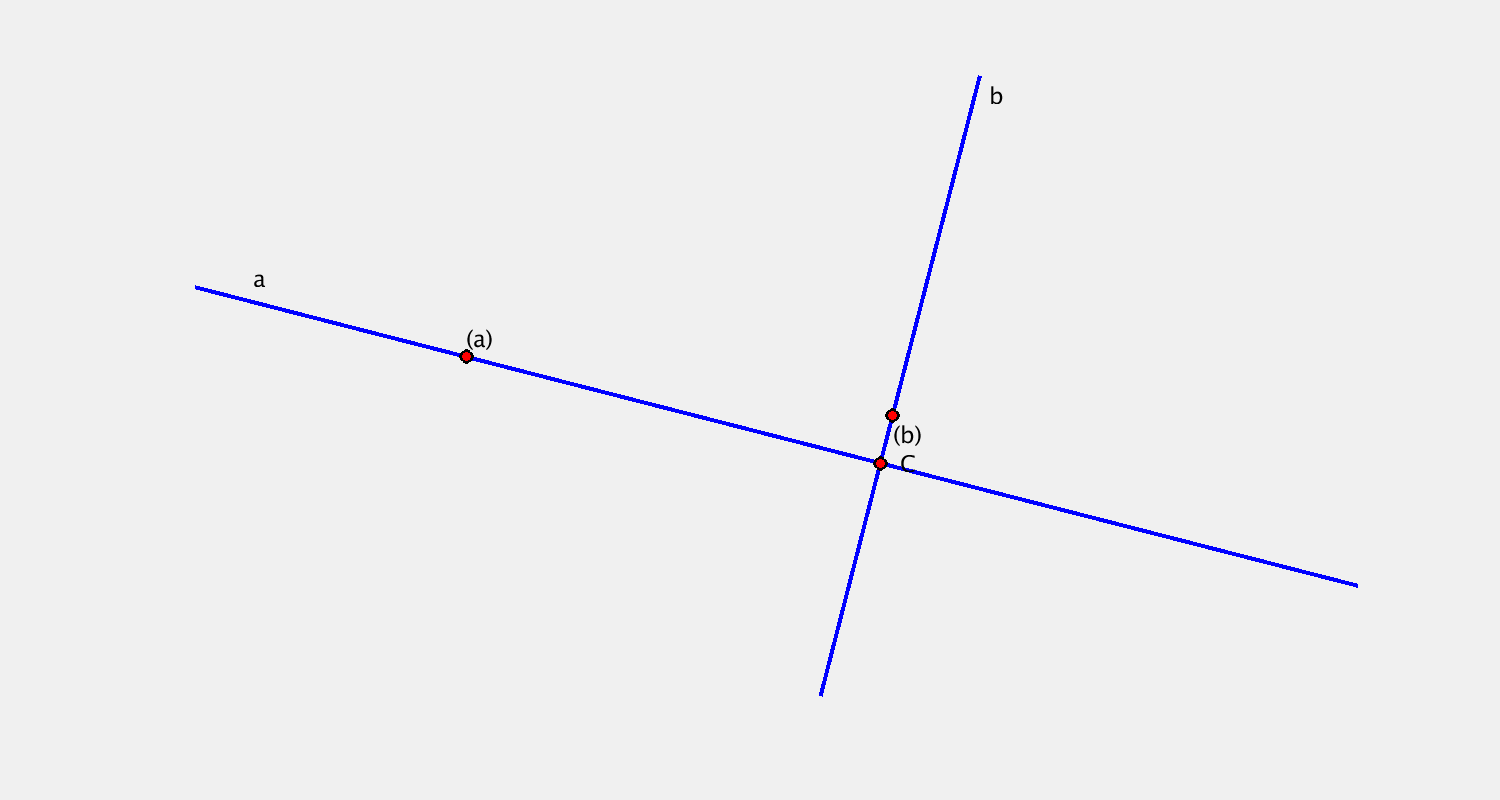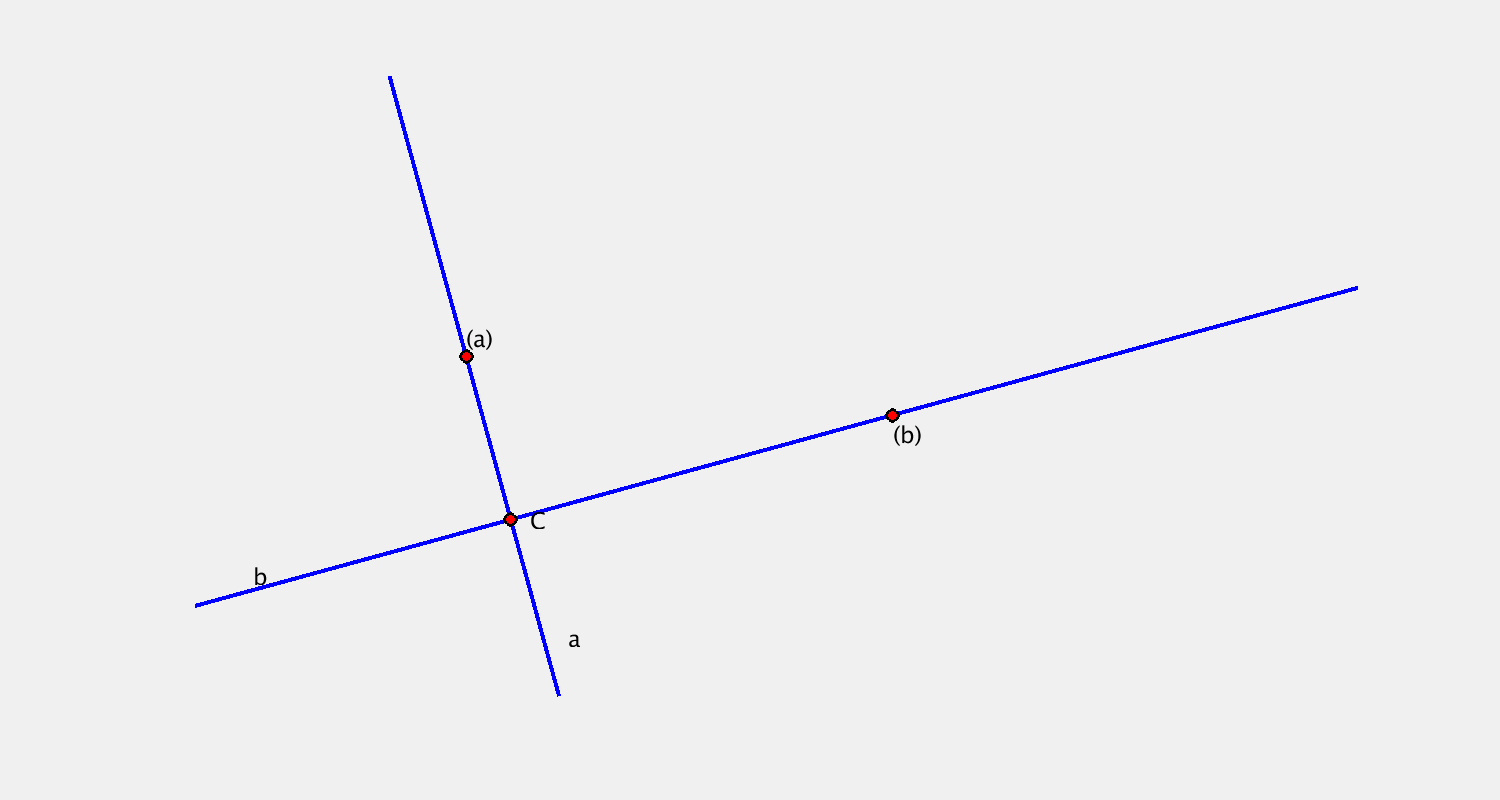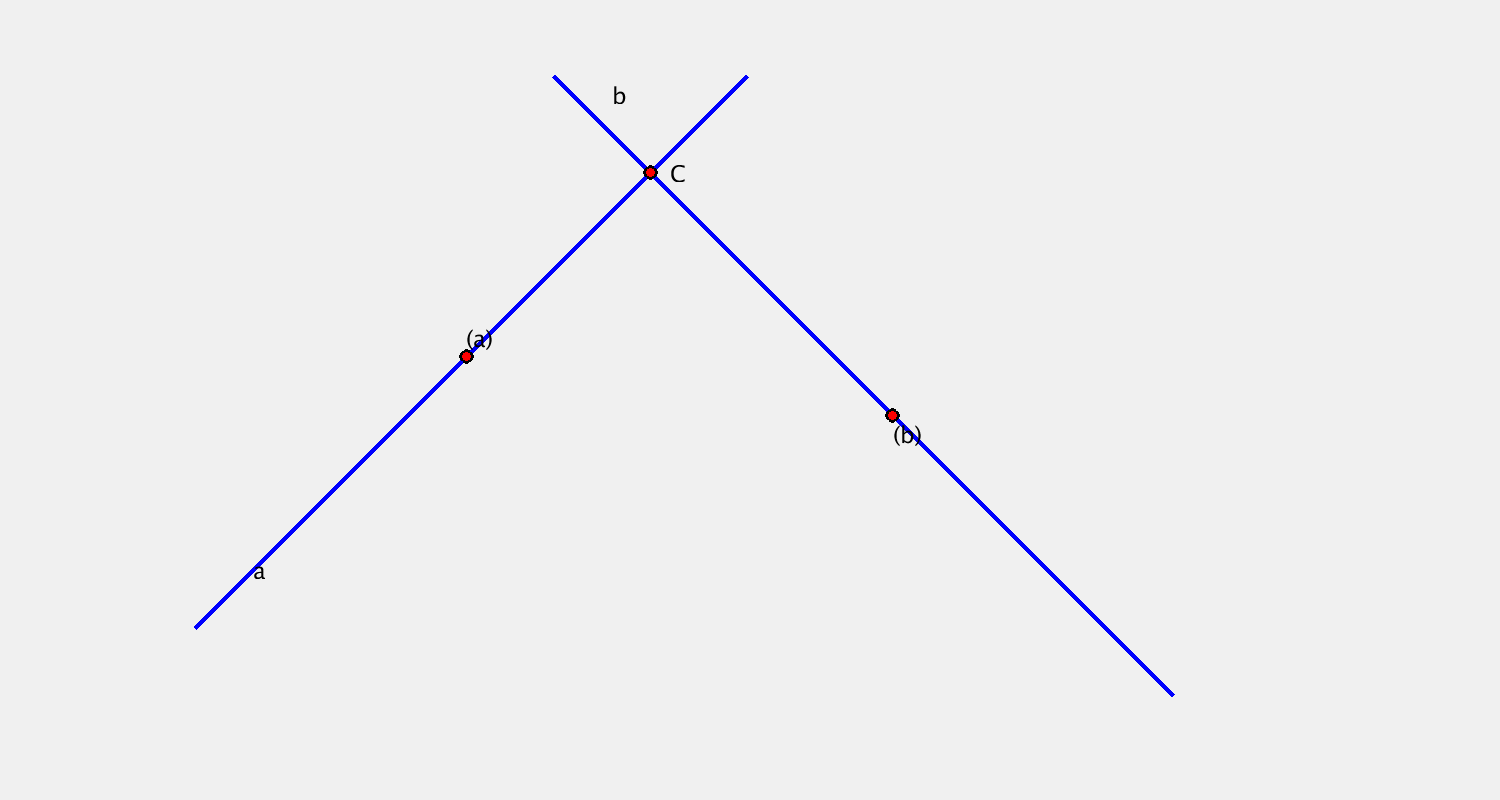
Příklad C
Pohyb je určen určen bodovou obálkou přímky $a$, kruhovou obálkou přímky $b$. Sestrojte další dvě polohy bodu $C$.
Elementární pohyb v rovině
- posunutí
- otáčení
Pozn.: posunutí → otáčení okolo středu "v nekonečnu"
Elementární pohyb v rovině
dvě polohy hybné soustavy $\sigma^1$ a $\sigma^2$ → existuje elementární pohyb, který převádí $\sigma^1$ do $\sigma^2$
elementární pohyb → otáčení
dva okamžiky "blízko sebe" → otáčení → okamžitý střed otáčení čili pól pohybu
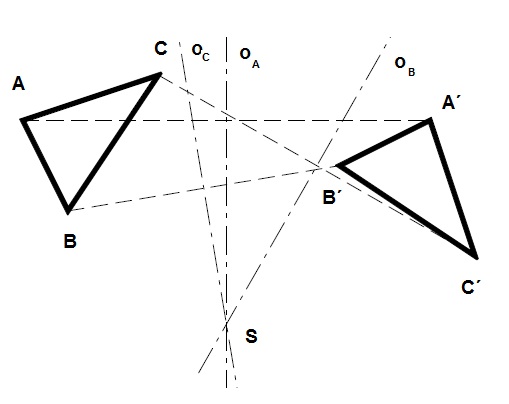
Pól pohybu (= okamžitý střed otáčení)
- průsečík všech normál trajektorií bodů a normál obálek křivek v daném okamžiku
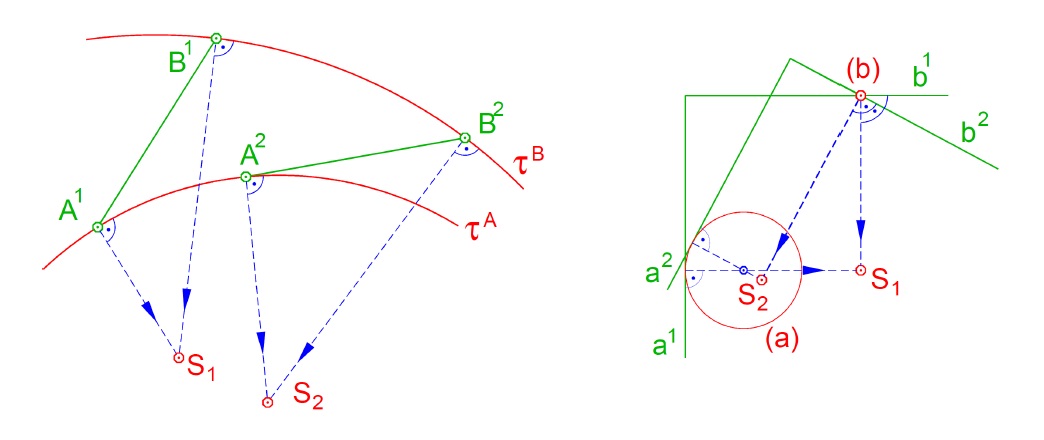
- vztah tečna ↔ normála
- pevná polodie
Příklad C
Sestrojte část trajektorie bodu $C$ včetně tečen k trajektorii ve zvolených polohách bodu $C$.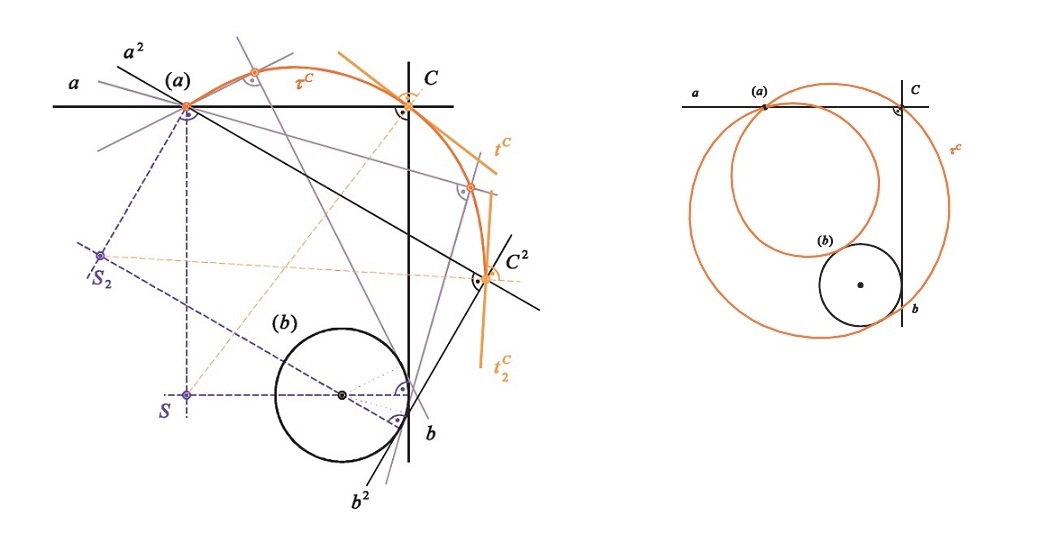
Pascalova závitnice
Příklad A
Sestrojte část obálky přímky $c$ včetně bodů dotyku obálky se zvolenými polohami přímky.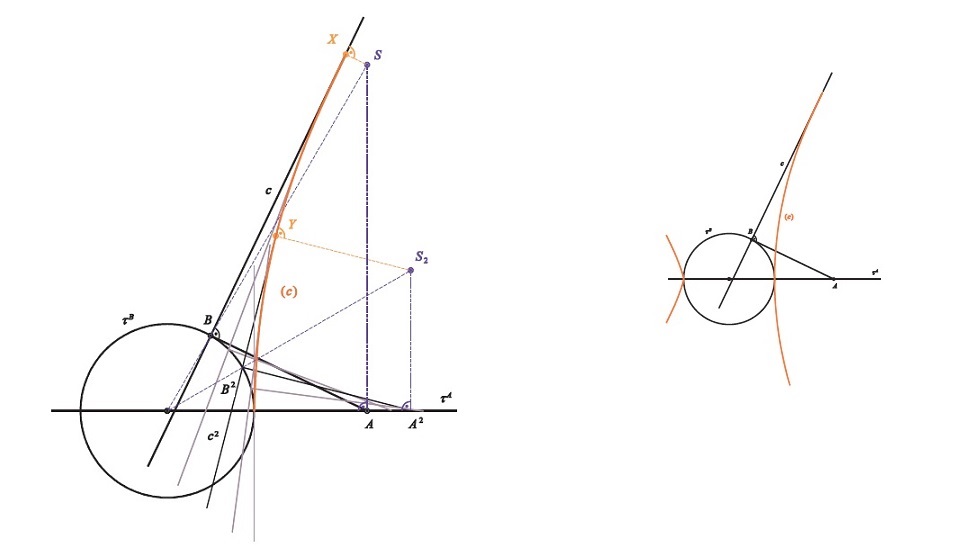
Příklad B
Sestrojte část obálky kružnice $k$ včetně bodů dotyku obálky se zvolenými polohami kružnice $k$.
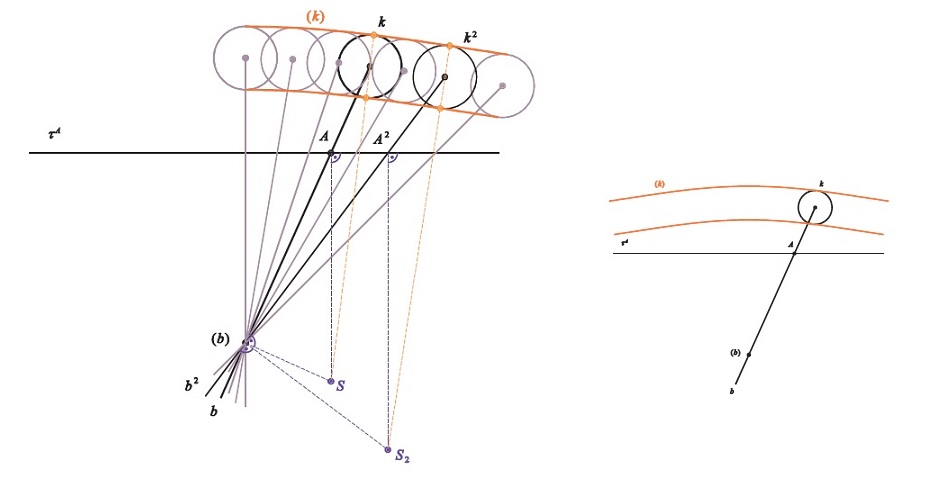
ekvidistanta Nikomedovy konchoidy
příště - hybná polodie, určení pohybu II
mat.fs.cvut.cz → Konstruktivní geometrie → Marta Hlavovázadání příkladů z přednášek (+ řešení)